Chapter 7 Spatial Models

7.1 Introduction

Many models assume that observations are obtained independently of each other. However, this is seldom the case. In Chapter 4 we have already seen how to account for correlated observations within groups. Distance between observations can also be a source of correlation. For example, in a city housing value usually changes smoothly between too contiguous neighborhoods. Pollution also shows a spatial smooth pattern and measurements close in space will likely be very similar. Also, the location of trees in a forest may follow a spatial pattern, depending on ground conditions, soil nutrients, etc.

All these examples have in common the spatial nature of the data. Observations that are close in space are likely to show similar values and a high degree of spatial autocorrelation. Spatial models will take into account this spatial autocorrelation in order to separate the general trend (usually depending on some covariates) from the purely spatial random variation.

Spatial statistics is traditionally divided into three main areas depending on the type of problem and data: lattice data, geostatistics and point patterns (Cressie 2015). Sometimes, spatial data is also measured over time and spatio-temporal models can be proposed (Cressie and Wikle 2011). In the next sections models for the different types of spatial data will be considered. In Section 8.6 models for spatio-temporal data will be described. Blangiardo and Cameletti (2015) and Krainski et al. (2018) provide a thorough description of most of the models described in this section. Bivand, Pebesma, and Gómez-Rubio (2013) and Lovelace, Nowosad, and Muenchow (2019) provide general description on handling spatial data in R and are recommended reads.

Spatial models for spatial data are introduced in Section 7.2. Geostatistical models for continuous spatial processes are presented in Section 7.3. Next, the analysis of point patterns is described in 7.4.

7.2 Areal data

Areal data, also known as lattice data, usually refers to data that are observed within given boundaries. For example, administrative boundaries are often used and the variables of study aggregated over these regions. Administrative boundaries will produce a lattice which will often have an irregular structure. Lattices with regular structures are difficult to find, but they may appear when spatial data come from an experiment (as described below).

In either case, spatial adjacency is often represented by a (sparse) adjacency matrix, with non-zero entries at the intersection of rows and columns of neighboring areas. This matrix will play an important role when building spatial models as spatial correlation structures will be built upon it. In particular, spatially correlated random effects will be modeled using a multivariate Gaussian distribution with a precision matrix that depends on an adjacency matrix.

7.2.1 Regular lattice

A regular lattice occurs when areas are structured as a matrix in rows and columns. It is often the case that spatial data is in a regular lattice as a result of an experimental design or data collection structure. For example, a regular lattice is a convenient way of modeling a count process, so that the study region is divided into small squares and the number of events in each cell is recorded. Because of the spatially inhomogeneous distribution of the events, cells which are neighbors will tend to have a similar number of events and this is how spatial autocorrelation appears in these data.

The bei dataset in the spatstat package (Baddeley, Rubak, and Turner 2015) records the locations of 3605 trees in a tropical rain forest (Condit 1998; Condit, Hubbell, and Foster 1996; Hubbell and Foster 1983; Møller and Waagepetersen 2007). This is stored as a ppp object, that essentially contains the boundary of the study region, a \(1000 \times 500\) meters region in this case, and the coordinates of the points. Furthermore, the bei.extra dataset includes the elevation and slope in the study region. These are available as im objects, which are raster images that cover the study area. Each raster is made of \(201\times 101\) pixels that represent the study area.

A regular lattice can be created from the original data by considering a matrix of \(5 \times 10\) squares in which the number of trees inside is computed. The following code makes extensive use of function in the sp and spatstat packages.

First of all, dataset bei is loaded and converted into a SpatialPoints object to represent the point pattern using classes in the sp package:

library("spatstat")
library("sp")
library("maptools")

data(bei)

# Create SpatialPoints object
bei.pts <- as(bei, "SpatialPoints")

Next, a grid over the rectangular study region is created to count the number of trees inside each of the cells in the grid:

#Create grid
bei.poly <- as(as.im(bei$window, dimyx=c(5, 10)), "SpatialGridDataFrame")
bei.poly <- as(bei.poly, "SpatialPolygons")

Function over() is used now to overlay the point pattern and the cells in the grid, so that the number of points in each cell of the grid is obtained.

#Number of observations per cell
idx <- over(bei.pts, bei.poly)
tab.idx <- table(idx)
#Add number of trees
d <- data.frame(Ntrees = rep(0, length(bei.poly)))
row.names(d) <- paste0("g", 1:length(bei.poly))
d$Ntrees[as.integer(names(tab.idx))] <- tab.idx

Finally, a SpatialPolygonsDataFrame is created by putting together the polygon representation of the cells in the grid and the number of trees in each cell:

#SpatialPolygonsDataFrame
bei.trees <- SpatialPolygonsDataFrame(bei.poly, d)

At this point, it is important to highlight how spatial data is internally stored in a SpatialGridDataFrame and the latent effects described in Table 7.1. For some models, INLA considers data sorted by column, i.e., a vector with the first column of the grid from top to bottom, followed by the second column and so on. In order to have this mapping we need to reorder the data as follows:

#Mapping
idx.mapping <- as.vector(t(matrix(1:50, nrow = 10, ncol = 5)))
bei.trees2 <- bei.trees[idx.mapping, ]

Figure 7.1 shows the order in which observations are internally stored in a SpatialGridDataFrame and how they are considered by the models in Table 7.1.

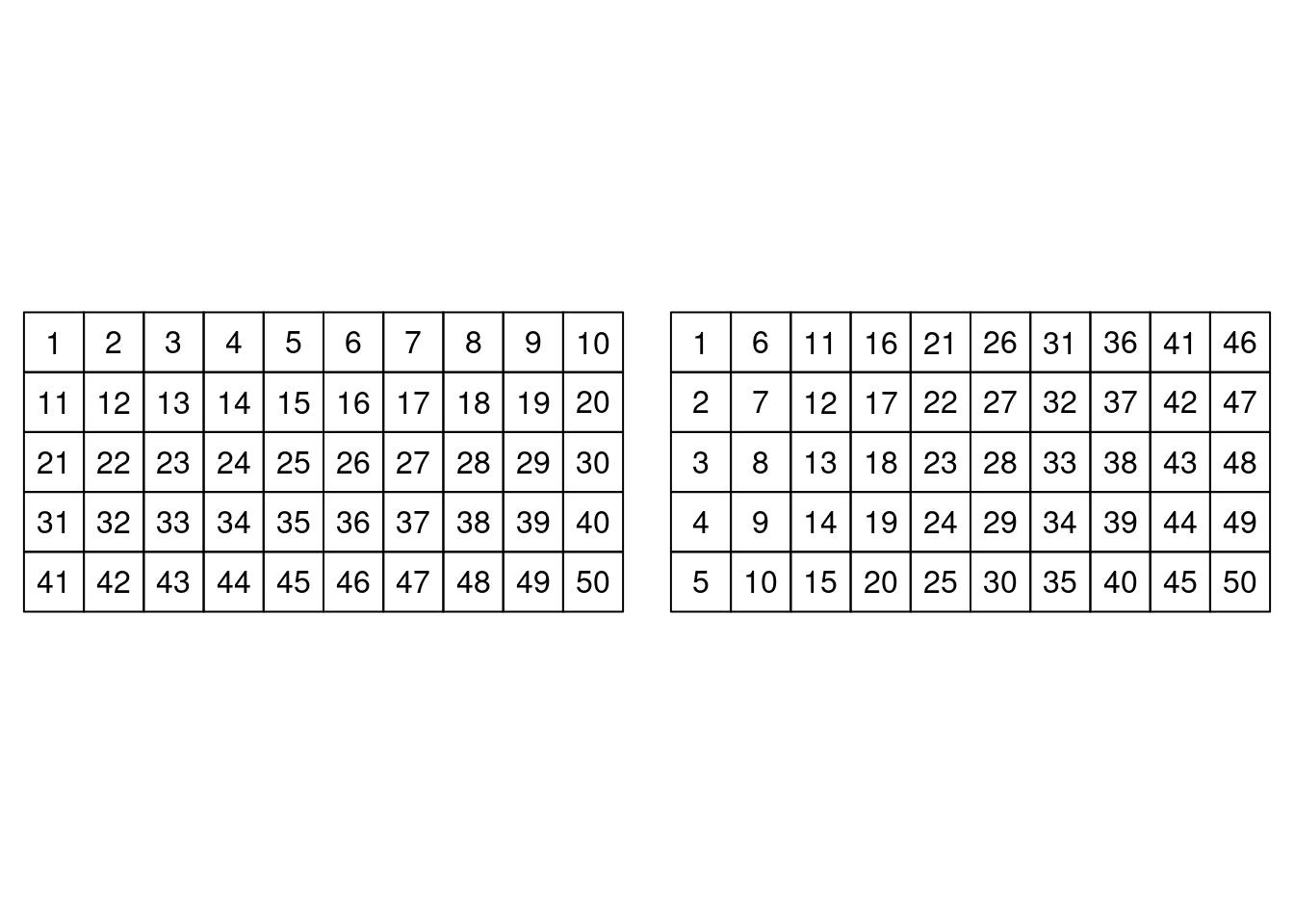
Mapping of cells in a SGDF (left) and mapping required by `INLA` (right).

Figure 7.1: Mapping of cells in a SGDF (left) and mapping required by INLA (right).

Figure 7.2 represents the cells into which we have divided the study region, that have been colored according to the number of trees inside. Furthermore, the actual location of the points has been plotted as an extra spatial layer to assess that the counts are correct.

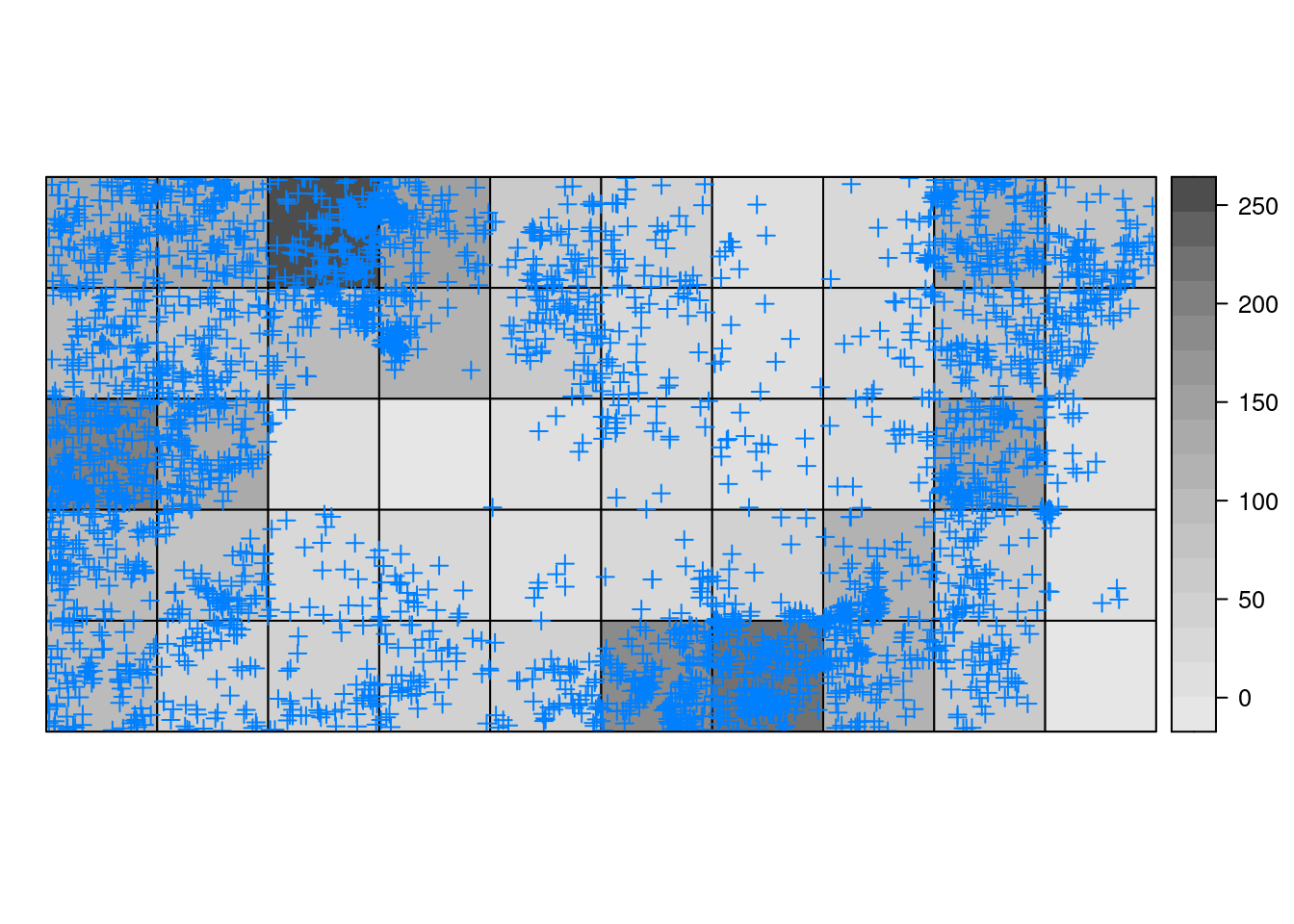
Spatial distribution of trees in a rain forest.

Figure 7.2: Spatial distribution of trees in a rain forest.

In addition to the counts, we will obtain summary statistics of the covariates to be used in our model fitting.

#Summary statistics of covariates
covs <- lapply(names(bei.extra), function(X) {
  layer <- bei.extra[[X]]
    res <- lapply(1:length(bei.trees2), function(Y) {
      summary(layer[as.owin(bei.trees2[Y, ])])})
    res <- as.data.frame(do.call(rbind, res))

    names(res) <- paste0(X, ".", c("min", "1Q", "2Q", "mean", "3Q", "max"))
    return(res)
    })

covs <- do.call(cbind, covs)

#Add to SPDF
bei.trees2@data <- cbind(bei.trees2@data, covs)

Figure 7.3 shows the average values of the elevation and gradient in the cells. When areal data are considered, aggregating individual data over areas is useful to build regression models. However, this aggregation process may blur the underlying point process.

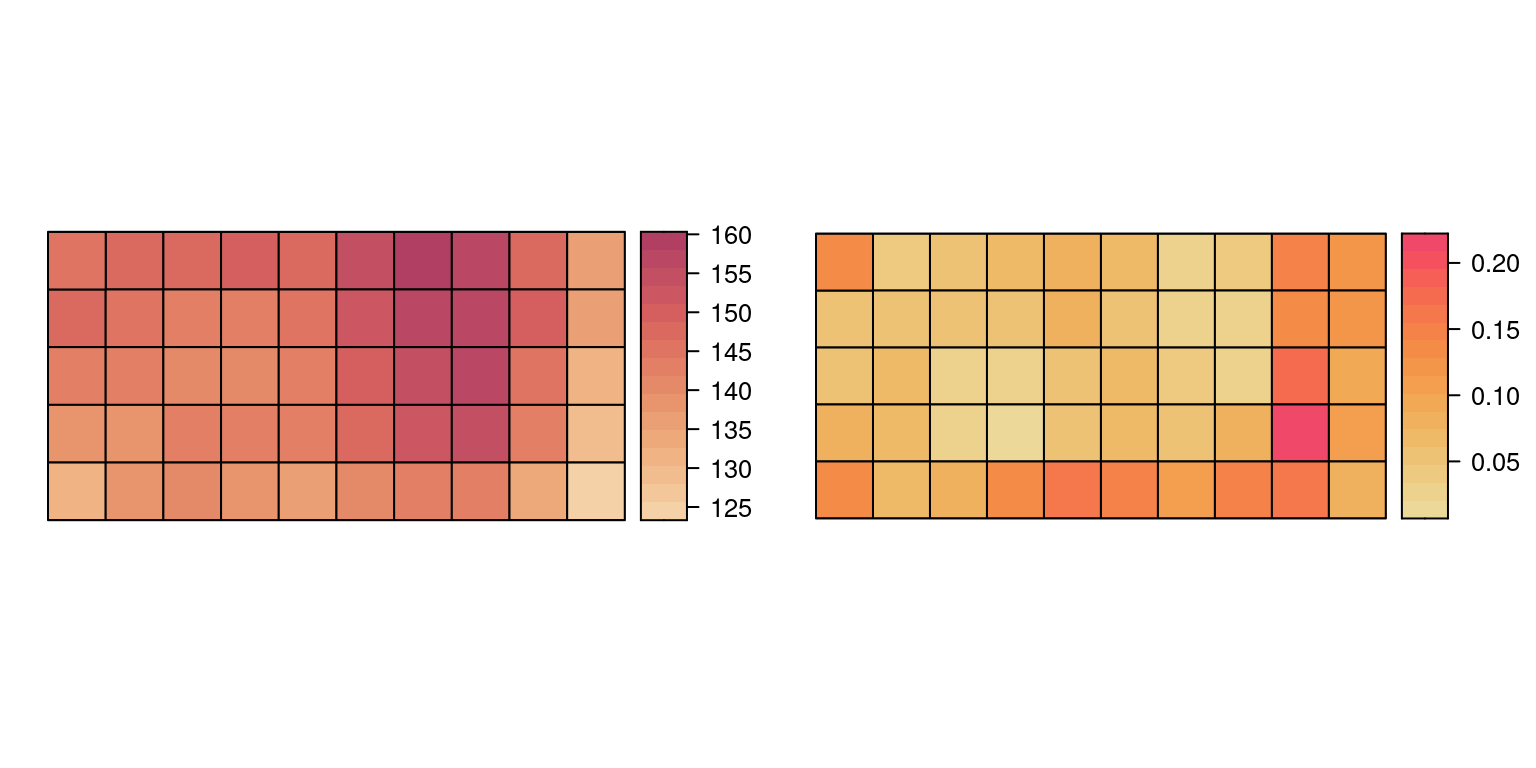
Average values of elevation (left) and gradient (right).

Figure 7.3: Average values of elevation (left) and gradient (right).

Spatial models for lattice data are often defined as random effects with a variance-covariance structure that depends on the neighborhood structure of the areas. In general, two areas will be neighbors if they share some boundaries. This could be just a single point (i.e., queen adjacency) or at least a segment (rook adjacency). For the current dataset, this is illustrated in Figure 7.4. The neighborhood structure has been obtained with function poly2nb from package spdep (Bivand and Wong 2018), which will return an nb object.

library("spdep")
library("spatialreg")
bei.adj.q <- poly2nb(bei.trees2)
bei.adj.r <- poly2nb(bei.trees2, queen = FALSE)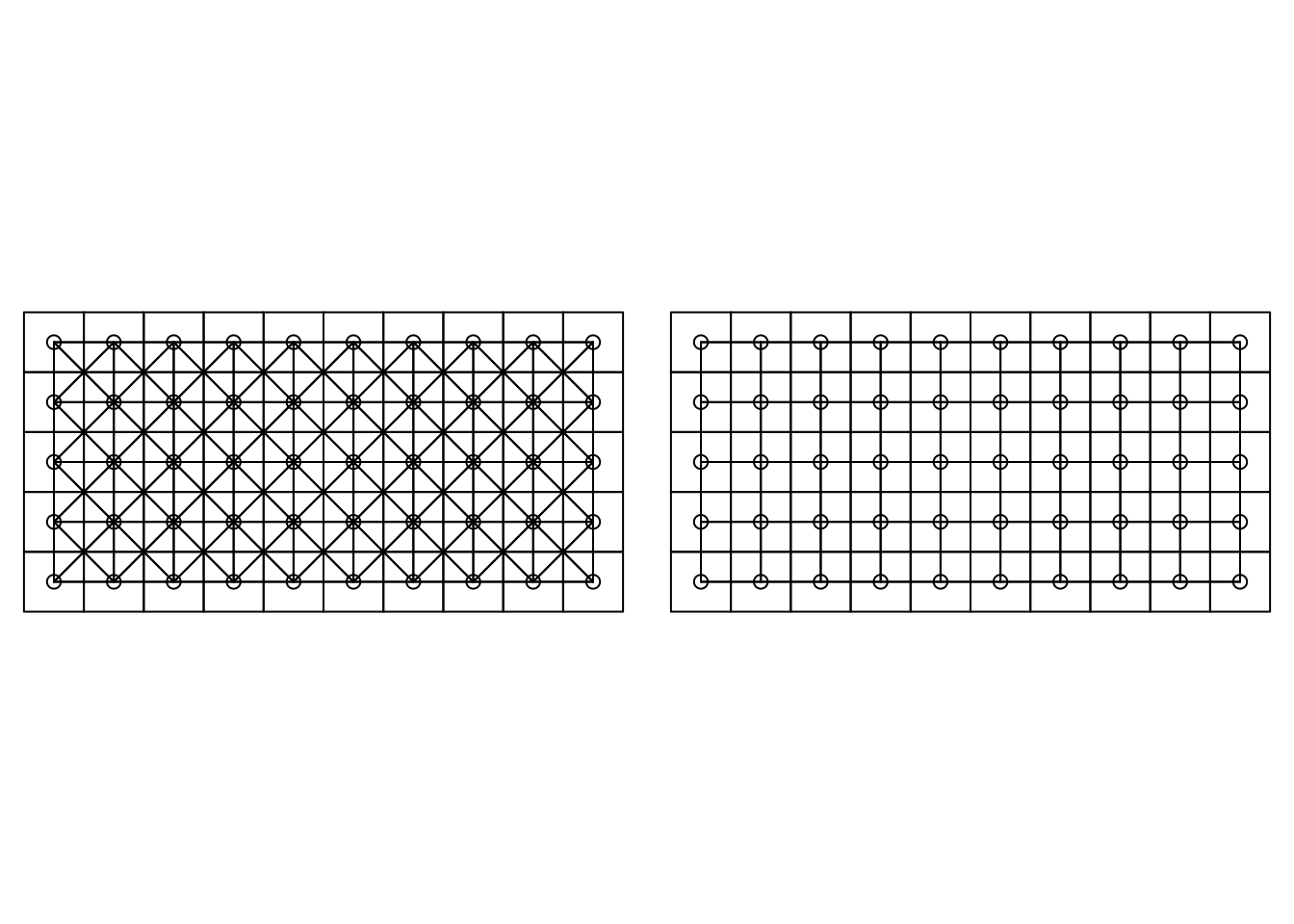
Queen (left) versus rook (right) adjacency.

Figure 7.4: Queen (left) versus rook (right) adjacency.

For \(n\) regions, adjacency can be represented as a \(n \times n\) matrix with non-zero entries if the regions in that row and column are neighbors. This is often represented as a binary indicator, but other types of weights can be used. Function nb2listw can be used to transform an nb object into a matrix of spatial weights using different specifications. A matrix of spatial weights will be denoted by \(W\).

The following code will create two adjacency matrices with binary weights (style = "B") and row-standardized (style = "W"), so that the values in each row sum up to one:

W.bin <- nb2listw(bei.adj.q, style = "B")
W.rs <- nb2listw(bei.adj.q, style = "W")
W.bin
## Characteristics of weights list object:
## Neighbour list object:
## Number of regions: 50 
## Number of nonzero links: 314 
## Percentage nonzero weights: 12.56 
## Average number of links: 6.28 
## 
## Weights style: B 
## Weights constants summary:
##    n   nn  S0  S1   S2
## B 50 2500 314 628 8488
W.rs
## Characteristics of weights list object:
## Neighbour list object:
## Number of regions: 50 
## Number of nonzero links: 314 
## Percentage nonzero weights: 12.56 
## Average number of links: 6.28 
## 
## Weights style: W 
## Weights constants summary:
##    n   nn S0    S1    S2
## W 50 2500 50 16.82 203.4

Spatial latent effects are multivariate Gaussian distribution with zero mean and precision matrix \(\tau \Sigma\), where \(\tau\) is an hyperparameter (i.e., the precision) and \(\Sigma\) a matrix that depends on the spatial adjacency matrix \(W\). Depending on the complexity of the spatial effect, matrix \(\Sigma\) may also depend on further hyperparameters (Banerjee, Carlin, and Gelfand 2014).

A summary of the main spatial latent effects available in INLA for regular lattice data is available in Table 7.1.

Table 7.1: Latent models in INLA for regular lattice data.
Model Precision
rw2d Random walk of order 2.
matern2d Gaussian field with Matérn correlation.

First of all, non-spatial models using the covariates and i.i.d. Gaussian random effects will be fit. This will serve as a baseline in order to assess whether spatial dependence is really needed in the model.

library("INLA")

#Log-Poisson regression
m0 <- inla(Ntrees ~ elev.mean + grad.mean, family = "poisson",
  data = as.data.frame(bei.trees2) )

#Log-Poisson regression with random effects
bei.trees2$ID <- 1:length(bei.trees2)
m0.re <- inla(Ntrees ~ elev.mean + grad.mean + f(ID), family = "poisson",
  data = as.data.frame(bei.trees2) )

As noted above, INLA assumes that the lattice is stored by columns, i.e., a vector with the first column, then followed by the second column and so on. Hence, a proper mapping between the spatial object with the data and the data.frame used in the call to inla is required.

In this case, data have already been reordered to the right mapping and the model can be fitted: 

#RW2d
m0.rw2d <- inla(Ntrees ~ elev.mean + grad.mean +
    f(ID, model = "rw2d", nrow = 5, ncol = 10),
  family = "poisson", data = as.data.frame(bei.trees2),
  control.predictor = list(compute = TRUE),
  control.compute = list(dic = TRUE) )

summary(m0.rw2d)
## 
## Call:
##    c("inla(formula = Ntrees ~ elev.mean + grad.mean + f(ID, model = 
##    \"rw2d\", ", " nrow = 5, ncol = 10), family = \"poisson\", data = 
##    as.data.frame(bei.trees2), ", " control.compute = list(dic = 
##    TRUE), control.predictor = list(compute = TRUE))" ) 
## Time used:
##     Pre = 0.225, Running = 0.125, Post = 0.0244, Total = 0.374 
## Fixed effects:
##                mean    sd 0.025quant 0.5quant 0.975quant    mode kld
## (Intercept) -10.863 7.781    -26.360  -10.821      4.391 -10.737   0
## elev.mean     0.094 0.053     -0.010    0.094      0.200   0.094   0
## grad.mean    12.652 3.566      5.619   12.648     19.704  12.638   0
## 
## Random effects:
##   Name     Model
##     ID Random walk 2D
## 
## Model hyperparameters:
##                   mean    sd 0.025quant 0.5quant 0.975quant mode
## Precision for ID 0.242 0.066      0.135    0.235      0.393 0.22
## 
## Expected number of effective parameters(stdev): 45.08(0.862)
## Number of equivalent replicates : 1.11 
## 
## Deviance Information Criterion (DIC) ...............: 385.18
## Deviance Information Criterion (DIC, saturated) ....: 109.38
## Effective number of parameters .....................: 45.27
## 
## Marginal log-Likelihood:  -319.68 
## Posterior marginals for the linear predictor and
##  the fitted values are computed

#Matern2D
m0.m2d <- inla(Ntrees ~ elev.mean + grad.mean +
    f(ID, model = "matern2d", nrow = 5, ncol = 10),
  family = "poisson", data = as.data.frame(bei.trees2),
  control.predictor = list(compute = TRUE) )

summary(m0.m2d)
## 
## Call:
##    c("inla(formula = Ntrees ~ elev.mean + grad.mean + f(ID, model = 
##    \"matern2d\", ", " nrow = 5, ncol = 10), family = \"poisson\", 
##    data = as.data.frame(bei.trees2), ", " control.predictor = 
##    list(compute = TRUE))") 
## Time used:
##     Pre = 0.228, Running = 0.225, Post = 0.0251, Total = 0.477 
## Fixed effects:
##               mean    sd 0.025quant 0.5quant 0.975quant   mode kld
## (Intercept) -8.463 3.977    -16.449   -8.415     -0.756 -8.320   0
## elev.mean    0.079 0.028      0.026    0.079      0.134  0.078   0
## grad.mean   14.119 3.347      7.595   14.092     20.793 14.040   0
## 
## Random effects:
##   Name     Model
##     ID Matern2D model
## 
## Model hyperparameters:
##                   mean   sd 0.025quant 0.5quant 0.975quant  mode
## Precision for ID 0.354 0.24      0.037    0.306      0.895 0.114
## Range for ID     8.063 5.50      3.294    6.377     22.747 4.223
## 
## Expected number of effective parameters(stdev): 45.94(0.719)
## Number of equivalent replicates : 1.09 
## 
## Marginal log-Likelihood:  -274.11 
## Posterior marginals for the linear predictor and
##  the fitted values are computed

Once the models have been fit, the posterior means of the fitted values are added to the SpatialPolygonsDataFame for plotting:

bei.trees2$RW2D <- m0.rw2d$summary.fitted.values[, "mean"]

bei.trees2$MATERN2D <- m0.m2d$summary.fitted.values[, "mean"]

As a summary of the fit models, Figure 7.5 shows the posterior means of the spatial random effects for the rw2d and matern2d models. The results support the hypothesis of a non-uniform distribution of the trees in the region.

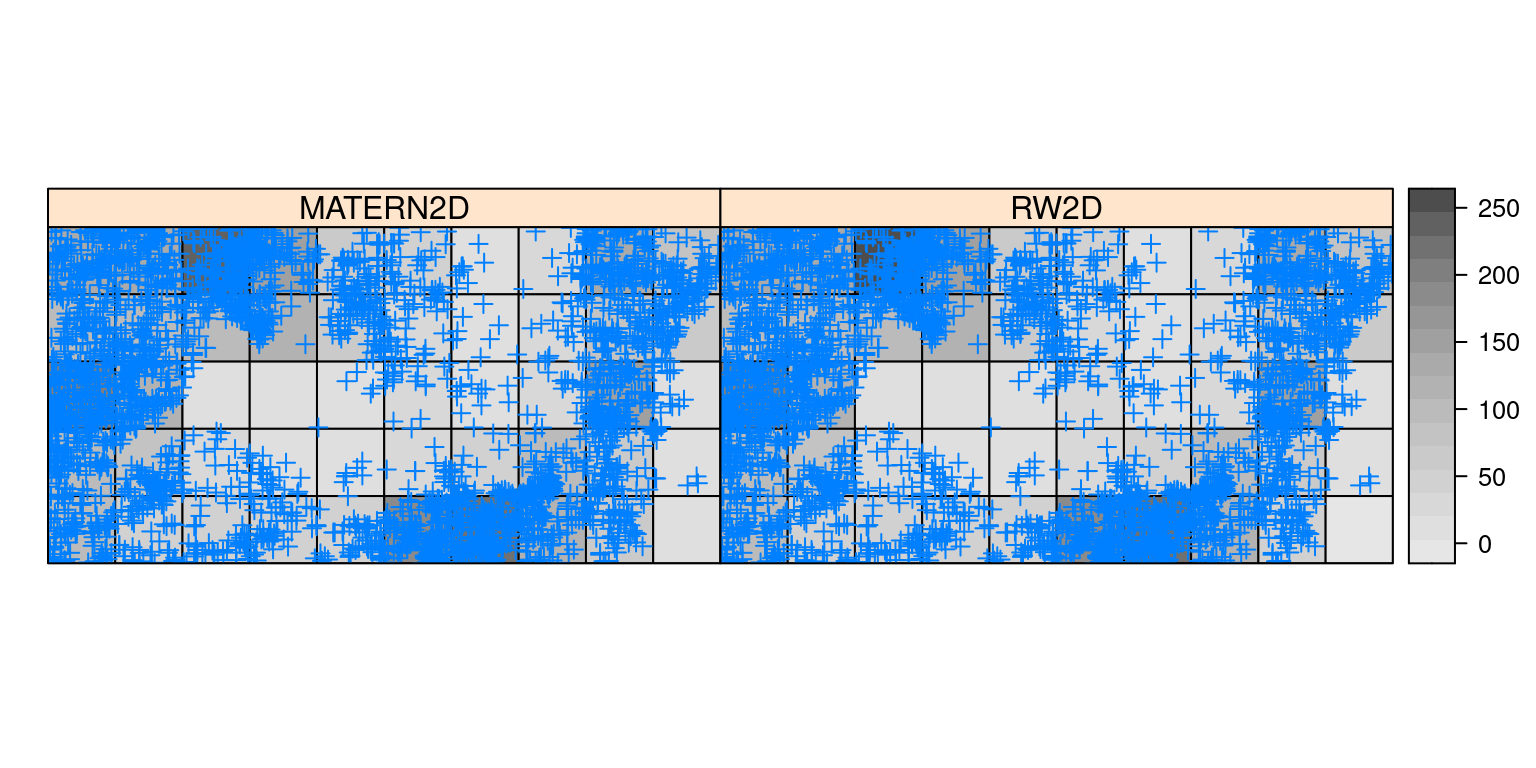
Posterior means of fitted values for regular lattices for the `bei` dataset.

Figure 7.5: Posterior means of fitted values for regular lattices for the bei dataset.

7.2.2 Irregular lattice

Lattice data are seldom in a regular grid. For example, administrative boundaries usually lead to an irregular lattice. The boston dataset, available in the spData package, records housing values in Boston census tracts (Harrison and Rubinfeld 1978) corrected for a few errors (Gilley and Pace 1996) and including longitude and latitude of the observations (Bivand 2017). Table 7.2 describes the variables in the dataset.

Table 7.2: Summary of some variables in the boston dataset, obtained from the its manual page.
Variable Description
TOWN Town name
CMEDV Corrected median of owner-occupied housing (in USD 1,000)
CRIM Crime per capita
ZN Proportions of residential land zoned for lots over 25,000 sq. ft per town
INDUS Proportions of non-retail business acres per town
CHAS Whether the tract borders Charles river (1 = yes, 0 = no)
NOX Nitric oxides concentration (in parts per 10 million)
RM Average number of rooms per dwelling
AGE Proportions of owner-occupied units built prior to 1940
DIS Weighted distances to five Boston employment centres
RAD Index of accesibility to radial highways per town
TAX Full-value property-tax rate per USD 10,000 per town
PTRATIO Pupil-teacher ratios per town
B \(1000*(Bk - 0.63)^2\), where \(Bk\) is the proportion of blacks
LSTAT Percentage values of lower status population

This dataset is available as a shapefile in the spData package, that can be loaded as follows:

library("rgdal")
boston.tr <- readOGR(system.file("shapes/boston_tracts.shp",
  package="spData")[1])

In order to compute the adjacency matrix, function poly2nb can be used:

boston.adj <- poly2nb(boston.tr)

By default, it will create a binary adjacency matrix, so that two regions are neighbors only if they share at least one point in common boundary (i.e., it is a queen adjacency). Figure 7.6 shows Boston census tracts in the data and the adjacency matrix.

Because of the irregular nature of the adjacency structure of the census tracts, the models introduced in the previous section cannot be used. Furthermore, binary and row-standardized adjacency matrices will be computed as they will be needed by the spatial models presented below:

W.boston <- nb2mat(boston.adj, style = "B") 
W.boston.rs <- nb2mat(boston.adj, style = "W")

This dataset contains a few censored observations in the response, which correspond to tracts with a higher median housing value then $50,000. For this reason, we will set all values equal to \(50.0\) to NA. This means that these areas will not be used for model fitting, but the predictive distribution will be computed by INLA so that inference on the housing value in these areas is still possible. See Section 12.3 for more details about how the predictive distribution is computed.

boston.tr$CMEDV2 <- boston.tr$CMEDV
boston.tr$CMEDV2 [boston.tr$CMEDV2 == 50.0] <- NA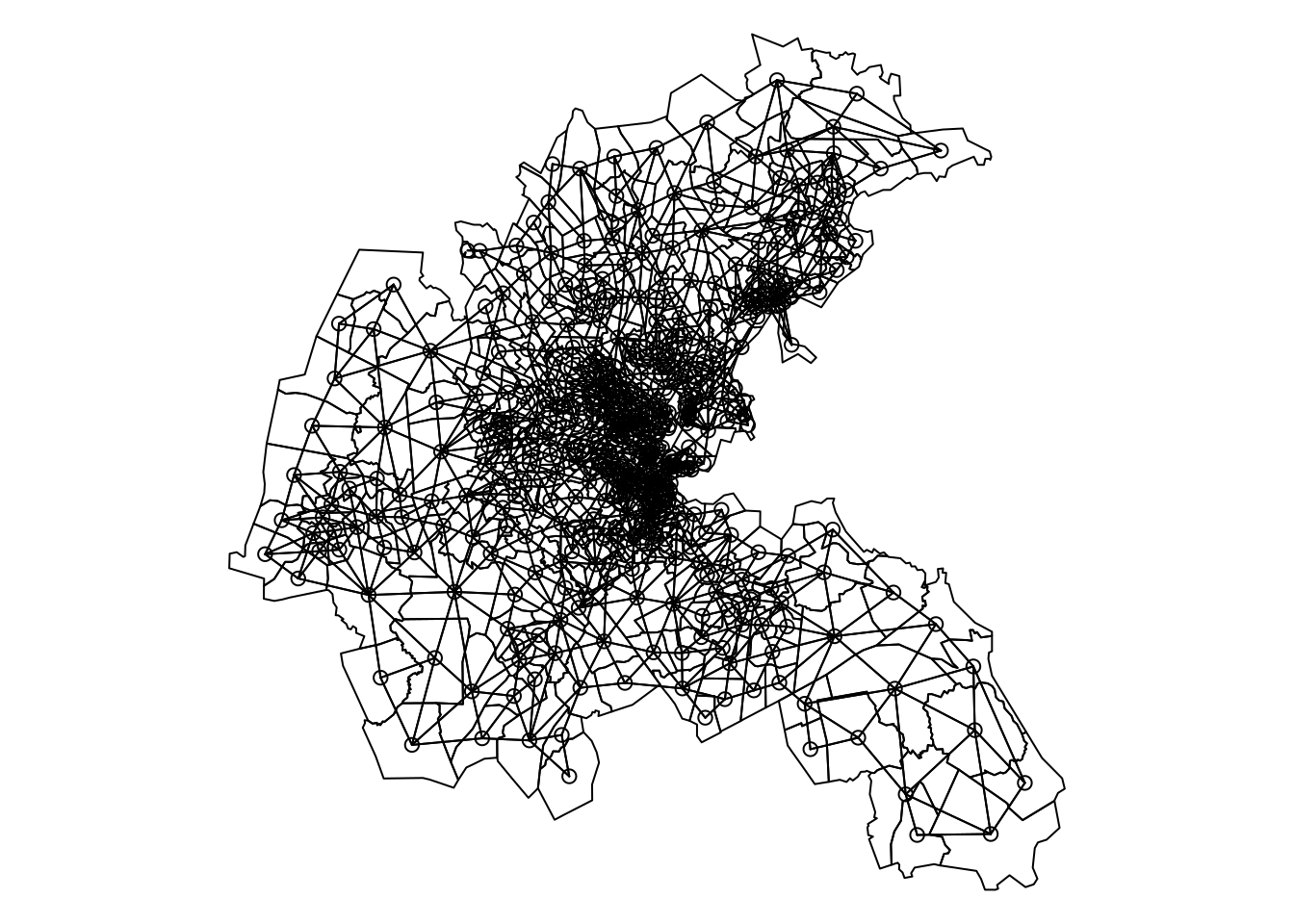
Boston tracts and adjacency matrix.

Figure 7.6: Boston tracts and adjacency matrix.

The model that we will be fitting will consider the response in the log-scale as this will make the response less skewed. The formula with the 13 covariates included in the model can be seen below. This is similar to the analysis performed in Harrison and Rubinfeld (1978) but other random effects will be considered as well to illustrate the use of the different models. In addition, a new column with the a region ID will be added to be used when defining random effects.

boston.form  <- log(CMEDV2) ~ CRIM + ZN + INDUS + CHAS + I(NOX^2) + I(RM^2) +
    AGE + log(DIS) + log(RAD) + TAX + PTRATIO + B + log(LSTAT)
boston.tr$ID <- 1:length(boston.tr)

First of all, a model with i.i.d. random effects will be fit to the data. This will provide a baseline to assess whether spatial random effects are really required when modeling these data. The estimates of the random effects (i.e., posterior means) will be added to the SpatialPolygonsDataFrame to be plotted later.

boston.iid <- inla(update(boston.form, . ~. + f(ID, model = "iid")),
  data = as.data.frame(boston.tr),
  control.compute = list(dic = TRUE, waic = TRUE, cpo = TRUE),
  control.predictor = list(compute = TRUE)
)
summary(boston.iid)
## 
## Call:
##    c("inla(formula = update(boston.form, . ~ . + f(ID, model = 
##    \"iid\")), ", " data = as.data.frame(boston.tr), control.compute = 
##    list(dic = TRUE, ", " waic = TRUE, cpo = TRUE), control.predictor 
##    = list(compute = TRUE))" ) 
## Time used:
##     Pre = 0.39, Running = 1.48, Post = 0.0545, Total = 1.92 
## Fixed effects:
##               mean    sd 0.025quant 0.5quant 0.975quant   mode kld
## (Intercept)  4.376 0.151      4.080    4.376      4.672  4.376   0
## CRIM        -0.011 0.001     -0.013   -0.011     -0.009 -0.011   0
## ZN           0.000 0.000     -0.001    0.000      0.001  0.000   0
## INDUS        0.001 0.002     -0.003    0.001      0.006  0.001   0
## CHAS1        0.056 0.034     -0.010    0.056      0.123  0.056   0
## I(NOX^2)    -0.540 0.107     -0.751   -0.540     -0.329 -0.540   0
## I(RM^2)      0.007 0.001      0.005    0.007      0.010  0.007   0
## AGE          0.000 0.001     -0.001    0.000      0.001  0.000   0
## log(DIS)    -0.143 0.032     -0.206   -0.143     -0.080 -0.143   0
## log(RAD)     0.082 0.018      0.047    0.082      0.118  0.082   0
## TAX          0.000 0.000     -0.001    0.000      0.000  0.000   0
## PTRATIO     -0.031 0.005     -0.040   -0.031     -0.021 -0.031   0
## B            0.000 0.000      0.000    0.000      0.001  0.000   0
## log(LSTAT)  -0.329 0.027     -0.382   -0.329     -0.277 -0.329   0
## 
## Random effects:
##   Name     Model
##     ID IID model
## 
## Model hyperparameters:
##                                             mean       sd 0.025quant
## Precision for the Gaussian observations    34.42     2.23      30.19
## Precision for ID                        18666.46 18355.20    1250.33
##                                         0.5quant 0.975quant    mode
## Precision for the Gaussian observations    34.36      38.98   34.27
## Precision for ID                        13249.17   67299.69 3412.82
## 
## Expected number of effective parameters(stdev): 18.53(10.17)
## Number of equivalent replicates : 26.45 
## 
## Deviance Information Criterion (DIC) ...............: -325.37
## Deviance Information Criterion (DIC, saturated) ....: 508.04
## Effective number of parameters .....................: 18.81
## 
## Watanabe-Akaike information criterion (WAIC) ...: -317.68
## Effective number of parameters .................: 25.46
## 
## Marginal log-Likelihood:  42.81 
## CPO and PIT are computed
## 
## Posterior marginals for the linear predictor and
##  the fitted values are computed

Note that the model is fit on the logarithm of CMEDV2. Hence, in order to make inference about CMEDV2 directly, the posterior marginals of the fitted values need to be transform with function inla.tmarginal() and then the posterior mean computed with inla.emarginal() (see Section 2.6 for details on manipulating marginals distributions). A new function tmarg()will be created to be used by other models as well. 

# Use 4 cores to process marginals in parallel
library("parallel")
options(mc.cores = 4)
# Transform marginals and compute posterior mean
#marginals: List of `marginals.fitted.values`from inla model
tmarg <- function(marginals) {
  post.means <- mclapply(marginals, function (marg) {
  # Transform post. marginals
  aux <- inla.tmarginal(exp, marg)
  # Compute posterior mean
  inla.emarginal(function(x) x, aux)
  })

  return(as.vector(unlist(post.means)))
}

# Add posterior means to the SpatialPolygonsDataFrame

boston.tr$IID <- tmarg(boston.iid$marginals.fitted.values)

Regarding spatial models for data in an irregular lattice, Table 7.3 summarizes some of the models available in INLA.

Table 7.3: Latent models in INLA for irregular lattice data.
Model Precision
besagproper Proper version of Besag’s spatial model
besag Besag’s spatial model (improper prior)
bym Convolution model, i.e., besag plus iid models

Three models will be considered: Besag’s proper spatial model, Besag’s improper spatial model and the one by Besag, York and Mollié, that is a convolution of an intrinsic CAR model and i.i.d. Gaussian model: 

#Besag's improper
boston.besag <- inla(update(boston.form, . ~. +
    f(ID, model = "besag", graph = W.boston)), 
  data = as.data.frame(boston.tr),
  control.compute = list(dic = TRUE, waic = TRUE, cpo = TRUE),
  control.predictor = list(compute = TRUE)
)
boston.tr$BESAG <- tmarg(boston.besag$marginals.fitted.values)


#Besag proper
boston.besagprop <- inla(update(boston.form, . ~. +
    f(ID, model = "besagproper", graph = W.boston)), 
  data = as.data.frame(boston.tr),
  control.compute = list(dic = TRUE, waic = TRUE, cpo = TRUE),
  control.predictor = list(compute = TRUE)
)
boston.tr$BESAGPROP <- tmarg(boston.besagprop$marginals.fitted.values)


#BYM
boston.bym <- inla(update(boston.form, . ~. +
    f(ID, model = "bym", graph = W.boston)), 
  data = as.data.frame(boston.tr),
  control.compute = list(dic = TRUE, waic = TRUE, cpo = TRUE),
  control.predictor = list(compute = TRUE)
)
boston.tr$BYM <- tmarg(boston.bym$marginals.fitted.values)

A convenient model when the aim is to assess spatial dependence in the data is the one proposed in Leroux, Lei, and Breslow (1999). In this model, the structure of the precision matrix is a convex combination of an identity matrix \(I\) (to represent i.i.d. spatial effect) and the precision of an intrinsic CAR \(Q\) (to represent a spatial pattern):

\[ (1 - \lambda) I + \lambda Q \]

Parameter \(\lambda\) lies between 0 and 1 and it controls the amount of spatial structure in the data. Small values indicate a non-spatial pattern, while large values indicate a strong spatial pattern.

Although this model is not directly implemented in INLA it can be noted that it is possible to fit this model using the generic1 (see Section 3.3) by taking matrix \(C\) equal to \(I - Q\), where \(Q\) is the precision matrix of an intrinsic CAR specification (Ugarte et al. 2014; Bivand, Gómez-Rubio, and Rue 2015).

Q <- Diagonal(x = sapply(boston.adj, length))
Q <- Q - as_dsTMatrix_listw(nb2listw(boston.adj, style = "B"))

C <- Diagonal(x = 1, n = nrow(boston.tr)) - Q
boston.ler <- inla(update(boston.form, . ~. +
    f(ID, model = "generic1", Cmatrix = C)),
  data = as.data.frame(boston.tr),
  control.compute = list(dic = TRUE, waic = TRUE, cpo = TRUE),
  control.predictor = list(compute = TRUE)
)
boston.tr$LER <- tmarg(boston.ler$marginals.fitted.values)

Figure 7.7 displays the observed values of CMEDV2 and the point estimates obtained with the different models. In the plot for CMEDV2 a few holes can be seen, which are filled with the prediction from the different models in the other plots. In the models with spatially correlated random effects this prediction is based on the covariates plus the spatially correlated random effects.

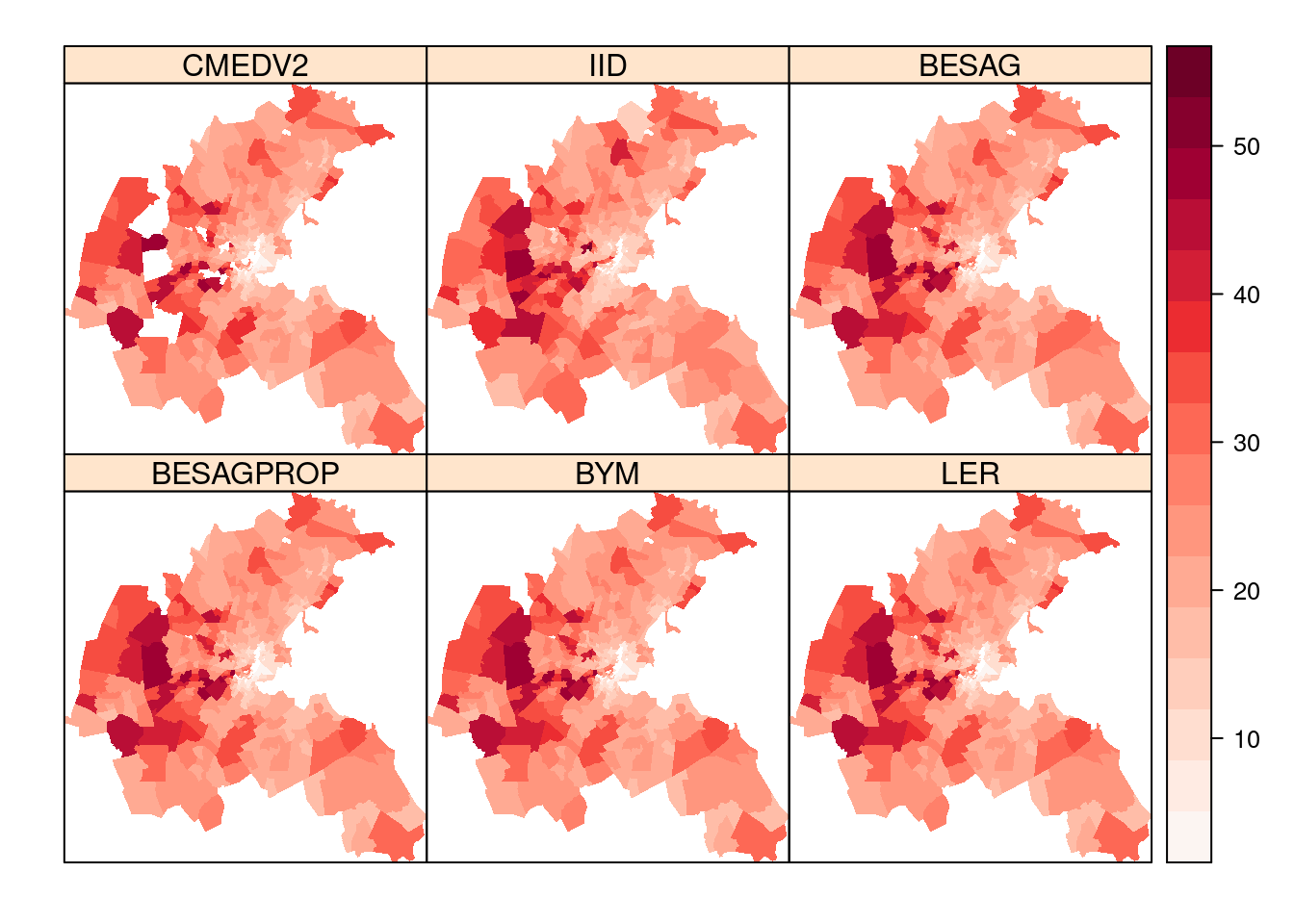
Summary of observed data and posterior means obtained with different models for the Boston housing dataset.

Figure 7.7: Summary of observed data and posterior means obtained with different models for the Boston housing dataset.

In general, all models provide similar posterior point estimates of the median housing value. For the areas with censored data, the predictive distributions also provide very similar estimates.

In terms of model selection criteria (see Section 2.4), Table 7.5 shows the different values for each model. All criteria point to the model by Leroux, Lei, and Breslow (1999) as the best one.

Table 7.4: Table: Table 7.5: Summary of model selection criteria of the models fit to the Boston housing dataset.
Model DIC WAIC CPO
iid -325.4 -317.7 -158.2
besag -2185.7 -2185.7 -692.8
besagproper -2694.7 -2694.7 -775.2
bym -2844.9 -2844.9 -953.4
leroux -2795.4 -2795.4 -909.4

Table: (#tab:bostonmodsel) Summary of model selection criteria of the models fit to the Boston housing dataset .

7.3 Geostatistics

Geostatistics deals with the analysis of continuous processes in space. A typical example is the spatial distribution of temperature or pollutants in the air. In this case, the variable of interest is only observed at a finite number of points and statistical methods are required for estimation all over the study region.

A geostatistical process is often represented as a continuous stochastic process \(y(x)\) with \(x\in \mathcal{D}\), where \(\mathcal{D}\) is the study region. This stochastic process is often assumed to follow a Gaussian distribution and \(y(x)\) is then called a Gaussian Process (GP, Cressie 2015).

In principle, dependence between two observations of the GP can be modeled by using an appropriate covariance function. However, quite often the GP is assumed to fulfill two important properties. First of all, the GP is assumed to be stationary, which means that the covariance between two points is the same even if they are shifted in space. Furthermore, the GP is assumed to be isotropic, which means that the correlation between two observations only depends on the distance between them. Making these two assumptions simplifies modeling of the geostatistics process as the covariance between two points will only depend on the relative distance between them regardless of their relative positions.

A commonly used covariance function is the Matérn covariance function (Cressie 2015). The covariance of two points which are a distance \(d\) apart is:

\[ C_{\nu} (d) = \sigma^2 \frac{2^{1 - \nu}}{\Gamma(\nu)} \left(\sqrt{2\nu}\frac{d}{\rho}\right)^{\nu} K_{\nu}\left(\sqrt{2\nu}\frac{d}{\rho}\right) \]

Here, \(\Gamma(\cdot)\) is the gamma function and \(K_{\nu}(\cdot)\) is the modified Bessel function of the second kind. Parameters \(\sigma^2\), \(\rho\) and \(\nu\) are non-negative values of the covariance function.

Parameter \(\sigma^2\) is a general scale parameter. The range of the spatial process is controlled by parameter \(\rho\). Large values will imply a fast decay in the correlation with distance, which imply a small range spatial process. Small values will indicate a spatial process with a large range. Finally, parameter \(\nu\) controls smoothness of the spatial process.

7.3.1 The meuse dataset

The meuse dataset in package gstat (Pebesma 2004) contains measurements of heavy metals concentrations in the fields next to the Meuse river, near the village of Stein (The Netherlands). In addition, the meuse.grid dataset records several of the covariates in the meuse dataset in a regular grid over the study region. These can be used in order to estimate the concentration of heavy metals at any point of the study region.

Table 7.6: Variables in the meuse dataset, obtained from its manual page.
Variable Description
x Easting (in meters).
y Northing (in meters).
cadmium Topsoil cadmium concentration (in ppm).
copper Topsoil copper concentration (in ppm).
lead Topsoil lead concentration (in ppm).
zinc Topsoil zinc concentration (in ppm).
elev Relative elevation above local river bed (in meters).
dist Distance to the Meuse river (normalized to \([0, 1]\)).
om Organic matter (in percentage).
ffreq Flooding frequency (1 = once in two years; 2 = once in ten years; 3 = once in 50 years).
soil Soil type (1 = Rd10A; 2 = Rd90C/VII; 3 = Bkd26/VII).
lime Lime class (0 = absent; 1 = present).
landuse Land use class.
dist.m Distance to the river (in meters).

These two datasets can be loaded by following the commands listed in their respective manual pages:

library("gstat")
data(meuse)

summary(meuse)
##        x                y             cadmium          copper     
##  Min.   :178605   Min.   :329714   Min.   : 0.20   Min.   : 14.0  
##  1st Qu.:179371   1st Qu.:330762   1st Qu.: 0.80   1st Qu.: 23.0  
##  Median :179991   Median :331633   Median : 2.10   Median : 31.0  
##  Mean   :180005   Mean   :331635   Mean   : 3.25   Mean   : 40.3  
##  3rd Qu.:180630   3rd Qu.:332463   3rd Qu.: 3.85   3rd Qu.: 49.5  
##  Max.   :181390   Max.   :333611   Max.   :18.10   Max.   :128.0  
##                                                                   
##       lead            zinc           elev            dist       
##  Min.   : 37.0   Min.   : 113   Min.   : 5.18   Min.   :0.0000  
##  1st Qu.: 72.5   1st Qu.: 198   1st Qu.: 7.55   1st Qu.:0.0757  
##  Median :123.0   Median : 326   Median : 8.18   Median :0.2118  
##  Mean   :153.4   Mean   : 470   Mean   : 8.16   Mean   :0.2400  
##  3rd Qu.:207.0   3rd Qu.: 674   3rd Qu.: 8.96   3rd Qu.:0.3641  
##  Max.   :654.0   Max.   :1839   Max.   :10.52   Max.   :0.8804  
##                                                                 
##        om        ffreq  soil   lime       landuse       dist.m    
##  Min.   : 1.00   1:84   1:97   0:111   W      :50   Min.   :  10  
##  1st Qu.: 5.30   2:48   2:46   1: 44   Ah     :39   1st Qu.:  80  
##  Median : 6.90   3:23   3:12           Am     :22   Median : 270  
##  Mean   : 7.48                         Fw     :10   Mean   : 290  
##  3rd Qu.: 9.00                         Ab     : 8   3rd Qu.: 450  
##  Max.   :17.00                         (Other):25   Max.   :1000  
##  NA's   :2                             NA's   : 1

Next, we will create a SpatialPointsDataFrame and assign the data its coordinate reference system (obtained from the manual page):

coordinates(meuse) <- ~x+y
proj4string(meuse) <- CRS("+init=epsg:28992")

A similar operation will be performed on the grid. Note that now the resulting object is a SpatialPixelsDataFrame, which is one of the objects in the sp package to represent spatial grids:

#Code from gstat
data(meuse.grid)
coordinates(meuse.grid) = ~x+y
proj4string(meuse.grid) <- CRS("+init=epsg:28992")
gridded(meuse.grid) = TRUE

Note that function proj4string is used to set the correct coordinate reference system (CRS) for the data, which essentially sets the units of the coordinates of the points as these do not necessarily need to be longitude and latitude. In this case, the CRS is Netherlands topographical map coordinates and they are measured in meters.

7.3.2 Kriging

As a preliminary analysis of this dataset, kriging will be used to obtain an estimation of the concentration of zinc in the study region. In particular, universal kriging (Cressie 2015; Bivand, Pebesma, and Gómez-Rubio 2013) will be used in order to include covariates in the prediction.

First of all, the empirical variogram will be computed using function variogram() and a spherical variogram fitted using function fit.variogram.

# Variogram and fit variogram
vgm <- variogram(log(zinc) ~ dist, meuse)
fit.vgm <- fit.variogram(vgm, vgm("Sph"))

Next, universal kriging will provide an estimate of the concentration of zinc at all points of the grid defined in meuse.grid. In addition to the point estimates, the square root of the prediction variance (which can be used as a measure of the error in the prediction) will be added as well.

# Kriging
krg <- krige(log(zinc) ~ dist, meuse, meuse.grid, model = fit.vgm)
## [using universal kriging]
#Add estimates to meuse.grid
meuse.grid$zinc.krg <- krg$var1.pred
meuse.grid$zinc.krg.sd <- sqrt(krg$var1.var)

Figure 7.8 shows the concentration of zinc, in the log-scale, estimated using universal kriging. The plot shows a clear spatial pattern, with higher concentrations in points closer to the Meuse river. These estimates will be compared later to other estimates obtained with spatial models fit with INLA. Note that the standard errors of the estimates have been computed and will be compared later to their analogous Bayesian estimates.

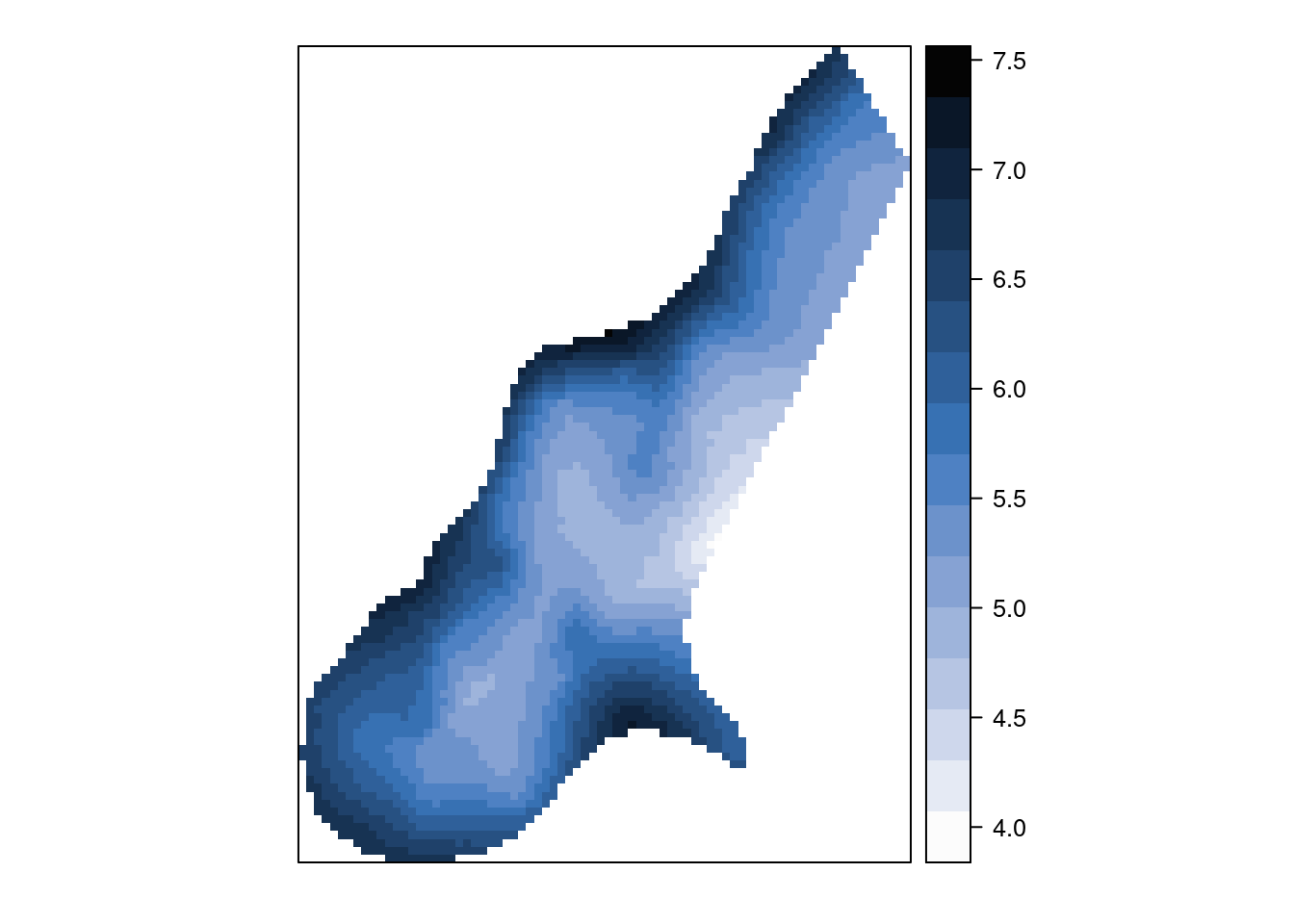
Concentration of zinc (log-scale) estimated with universal kriging for the `meuse` dataset.

Figure 7.8: Concentration of zinc (log-scale) estimated with universal kriging for the meuse dataset.

7.3.3 Spatial Models using Stochastic Partial Differential Equations

Continuous spatial processes using a Matérn covariance function can be easily fitted with INLA. Lindgren, Rue, and Lindström (2011) note that a spatial process with a Matérn covariance can be obtained as the weak solution to a stochastic partial differential equation (SPDE). Hence, they provide a solution to the equation and they are able to work with a sparse representation of the solution that fits within the INLA framework.

The solution \(u(s)\) can be represented as:

\[ u(s) = \sum_{k=1}^K \psi_k(s)w_k,\ s\in\mathcal{D} \]

In the previous equation, \(\{\psi_k(s)\}_{k=1}^K\) is a basis of functions needed to approximate the solution and \(w_k\) are associate coefficients, which are assumed to have a Gaussian distribution.

This spatial model is implemented as the spde latent effect in INLA. However, defining this model to be used with INLA requires more work than previous spatial models. In particular, a mesh needs to be defined over the study region and it will be used to compute the approximation to the solution (i.e., the spatial process). Krainski et al. (2018) describe SPDE models in detail, but here we will summarize the different steps require to fit these models.

As a previous step, the boundary of the study region needs to be defined. For this, the boundaries of the pixels in the meuse.grid will be joined into a single region. This will provide a reasonable approximation to the boundary of the study region.

#Boundary
meuse.bdy <- unionSpatialPolygons(
  as(meuse.grid, "SpatialPolygons"), rep (1, length(meuse.grid))
)

Next, a two-dimensional mesh will be defined to define the set of basis functions using function inla.mesh.2d(). This will take the boundary of the study region, as well as the dimensions of the maximum edge of the triangles in the mesh and the length of the inner and outer offset. 

#Define mesh
pts <- meuse.bdy@polygons[[1]]@Polygons[[1]]@coords
mesh <- inla.mesh.2d(loc.domain = pts, max.edge = c(150, 500),
  offset = c(100, 250) )

Figure 7.9 displays the boundary of the study region and the mesh created to approximate the solution of the SPDE to obtain the spatial model. A thick line separates the outer offset from the inner offset and the boundary of the study region. The figure has been obtained with the following code:

This triangulation defines the basis of functions that will be used to approximate the spatial process with Matérn covariance. In particular, the basis of functions is defined such as each function is one at a given vertex and zero outside the triangles that meet at that vertex. Hence, the functions have a compact support and they decay linearly from the vertex (where the value is 1) to the the boundary of the support (where it takes a value of zero). This means that for any given triangle in the mesh, only three functions in the basis will have non-zero values, which simplifies the computation of the estimates of the random effect at any given point because its estimate will be a linear combination of only three functions in the basis. See Chapter 2 in Krainski et al. (2018) for full details on how the basis functions are defined].

par(mar = c(0, 0, 0, 0))
plot(mesh, asp = 1, main = "")
lines(pts, col = 3, with = 2)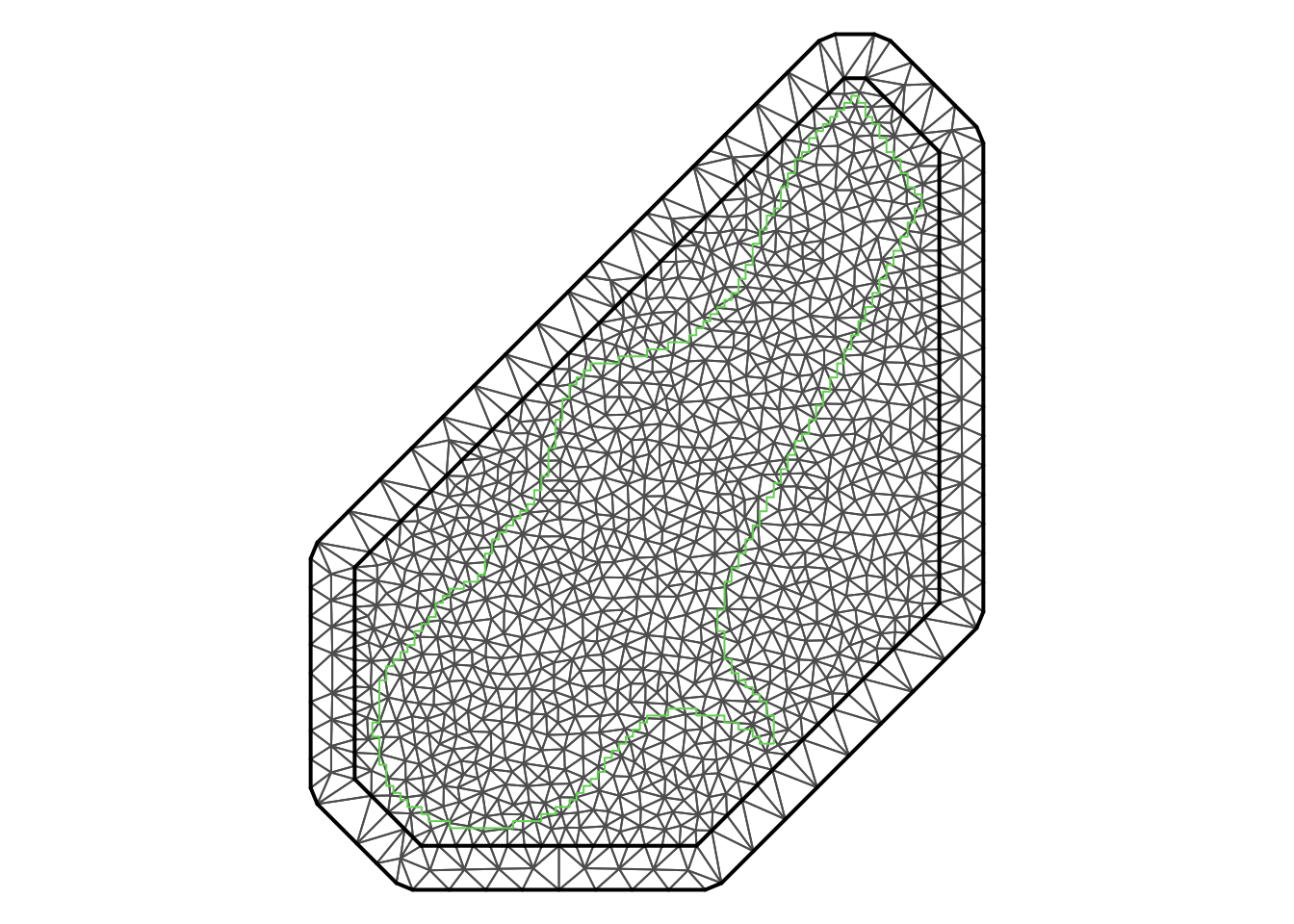
Mesh created for the analysis of the `meuse` dataset with INLA and SPDEs.

Figure 7.9: Mesh created for the analysis of the meuse dataset with INLA and SPDEs.

Function inla.spde2.matern() is used next to create an object for a Matérn model. Furthermore, inla.spde.make.A is also used to create the projector matrix \(A\) to map the projection of the SPDE to the observed points and inla.spde.make.index a necessary list of named index vectors for the SPDE model. 

#Create SPDE
meuse.spde <- inla.spde2.matern(mesh = mesh, alpha = 2)
A.meuse <- inla.spde.make.A(mesh = mesh, loc = coordinates(meuse))
s.index <- inla.spde.make.index(name = "spatial.field",
  n.spde = meuse.spde$n.spde)

The previous steps will define how the solution to the SPDE that defined the spatial process with a Matérn covariance is computed. This will be used later when defining the spatial random effect using the f() function in the formula that defines the INLA model.

Data passed to inla() when a SPDE is used needs to be in a particular format. For this, the inla.stack function is provided. It will take data in different ways, including the SPDE indices, and arrange them conveniently for model fitting. In short, inla.stack will be a list with the following named elements:

  • data: a list with data vectors.

  • A: a list of projector matrices.

  • effects: a list of effects (e.g., the SPDE index) or predictors (i.e., covariates).

  • tag: a character with a label for this group of data.

For example, in order to define the data to be used for model fitting, we could do the following:

#Create data structure
meuse.stack <- inla.stack(data  = list(zinc = meuse$zinc),
  A = list(A.meuse, 1),
  effects = list(c(s.index, list(Intercept = 1)),
    list(dist = meuse$dist)),
  tag = "meuse.data")

Here, data is simply a list with a vector of the values of zinc. A is a list with projector matrix A.meuse (used in the spatial model) and the value \(1\). These two elements are associated with the two elements in effects, which is a list of some information about the definition of the SPDE and some effects with covariate dist. Finally, tag is a label to indicate that this is the data in the meuse dataset.

This is all that is required to fit the model with an intercept, a covariate (distance to the river) plus the spatial random effect defined with a SPDE. However, given that we are studying a continuous spatial process, obtaining an estimate of the variable of interest (and the underlying spatial effect) in the study region is of interest.

For this reason, another stack of data can be defined for prediction. In this case, the values of the response variable will be set to NA and the predictive distributions computed. In addition, a different projector matrix will be required in order to map the estimates of the spatial process to the prediction points. This can be done using function inla.spde.make.A as before using the points in the grid. 

#Create data structure for prediction
A.pred <- inla.spde.make.A(mesh = mesh, loc = coordinates(meuse.grid))
meuse.stack.pred <- inla.stack(data = list(zinc = NA),
  A = list(A.pred, 1),
  effects = list(c(s.index, list (Intercept = 1)),
    list(dist = meuse.grid$dist)),
  tag = "meuse.pred")

Note that now a different tag ("meuse.pred") has been used in order to be able to identify this part of the data in the stack to retrieve the fitted values and other quantities of interest at the grid points.

Finally, both stacks of data can be put together into a single object with inla.stack again. The resulting object will be the one passed to function inla when fitting the model. 

#Join stack
join.stack <- inla.stack(meuse.stack, meuse.stack.pred)

To define the model that will be fitted, the spatial effects need to be added using the f() function. The index passed to this function will be the one created before with inla.spde.make.index and whose name is spatial.field. In addition, the model will be of type spde. 

#Fit model
form <- log(zinc) ~ -1 + Intercept + dist + f(spatial.field, model = spde)

Data passed to the inla function needs to be joined with the definition of the SPDE to fit the spatial model. This is done with function inla.stack.data. Furthermore, control.predictor will need to take the projector matrix for the whole dataset (model fitting and prediction) using function inla.stack.A in join.stack. 

m1 <- inla(form, data = inla.stack.data(join.stack, spde = meuse.spde),
  family = "gaussian",
  control.predictor = list(A = inla.stack.A(join.stack), compute = TRUE),
  control.compute = list(cpo = TRUE, dic = TRUE))

#Summary of results
summary(m1)
## 
## Call:
##    c("inla(formula = form, family = \"gaussian\", data = 
##    inla.stack.data(join.stack, ", " spde = meuse.spde), 
##    control.compute = list(cpo = TRUE, dic = TRUE), ", " 
##    control.predictor = list(A = inla.stack.A(join.stack), compute = 
##    TRUE))" ) 
## Time used:
##     Pre = 0.405, Running = 66.9, Post = 0.519, Total = 67.8 
## Fixed effects:
##             mean    sd 0.025quant 0.5quant 0.975quant   mode kld
## Intercept  6.591 0.143      6.317    6.588      6.889  6.581   0
## dist      -2.808 0.380     -3.563   -2.807     -2.058 -2.805   0
## 
## Random effects:
##   Name     Model
##     spatial.field SPDE2 model
## 
## Model hyperparameters:
##                                          mean    sd 0.025quant 0.5quant
## Precision for the Gaussian observations 18.72 6.437       8.97    17.79
## Theta1 for spatial.field                 4.41 0.299       3.83     4.40
## Theta2 for spatial.field                -4.94 0.309      -5.57    -4.94
##                                         0.975quant  mode
## Precision for the Gaussian observations      33.94 16.02
## Theta1 for spatial.field                      5.01  4.38
## Theta2 for spatial.field                     -4.36 -4.91
## 
## Expected number of effective parameters(stdev): 88.80(17.55)
## Number of equivalent replicates : 1.75 
## 
## Deviance Information Criterion (DIC) ...............: 80.44
## Deviance Information Criterion (DIC, saturated) ....: 245.01
## Effective number of parameters .....................: 87.41
## 
## Marginal log-Likelihood:  -108.15 
## CPO and PIT are computed
## 
## Posterior marginals for the linear predictor and
##  the fitted values are computed

According to the model fitted there is a clear reduction in the concentration of zinc as distance to the river increases. This is consistent with previous findings and the results from the universal kriging.

Obtaining the fitted values at the prediction points requires first getting the index for the points in the meuse.pred part of the stack. This can be easily done with function inla.stack.index (see code below). Similarly, fitted values for the meuse.data can be obtained. Next, the index is used to obtain the posterior means and other summary statistics computed on the predictive distributions and these added to the meuse.grid object for plotting. 

#Get predicted data on grid
index.pred <- inla.stack.index(join.stack, "meuse.pred")$data

meuse.grid$zinc.spde <- m1$summary.fitted.values[index.pred, "mean"]
meuse.grid$zinc.spde.sd <- m1$summary.fitted.values[index.pred, "sd"]

Figure 7.10 shows the posterior means of the concentrations of zinc in the log-scale and Figure 7.11 the prediction standard deviations, which are a measure of the uncertainty about the predictions. Point estimates of the concentration seem to be very similar between universal kriging and the model fitted with INLA. However, prediction uncertainty seems to be smaller with the SPDE model. Note that here we are comparing results from two different inference methods. Furthermore, these differences in the uncertainty may be due to the different ways in which the covariance of the spatial effect is computed and a shrinkage effect due to the priors in the Bayesian model.

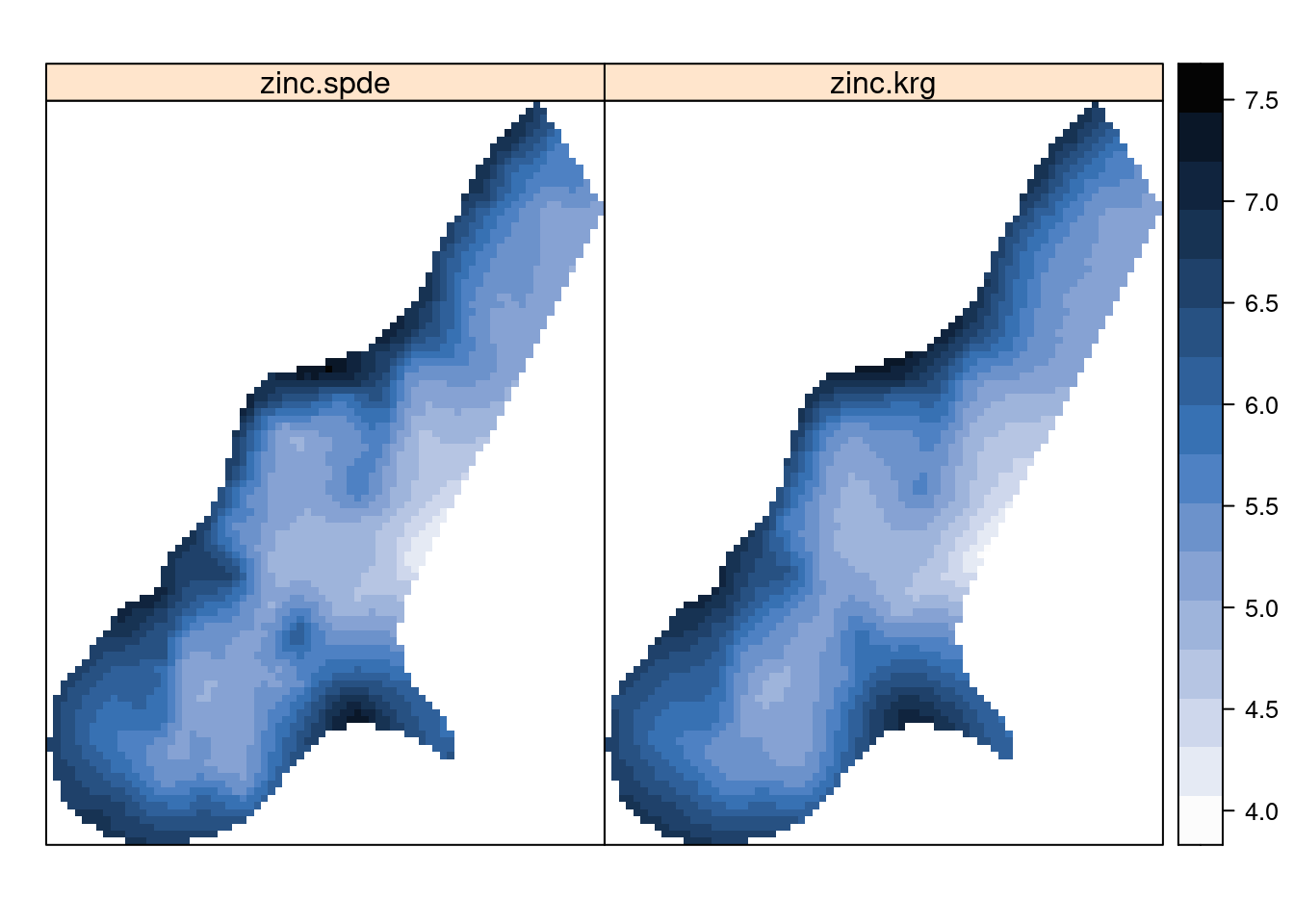
Posterior means of log-concentration of zinc.

Figure 7.10: Posterior means of log-concentration of zinc.

Posterior prediction standard deviations of log-concentration of zinc.

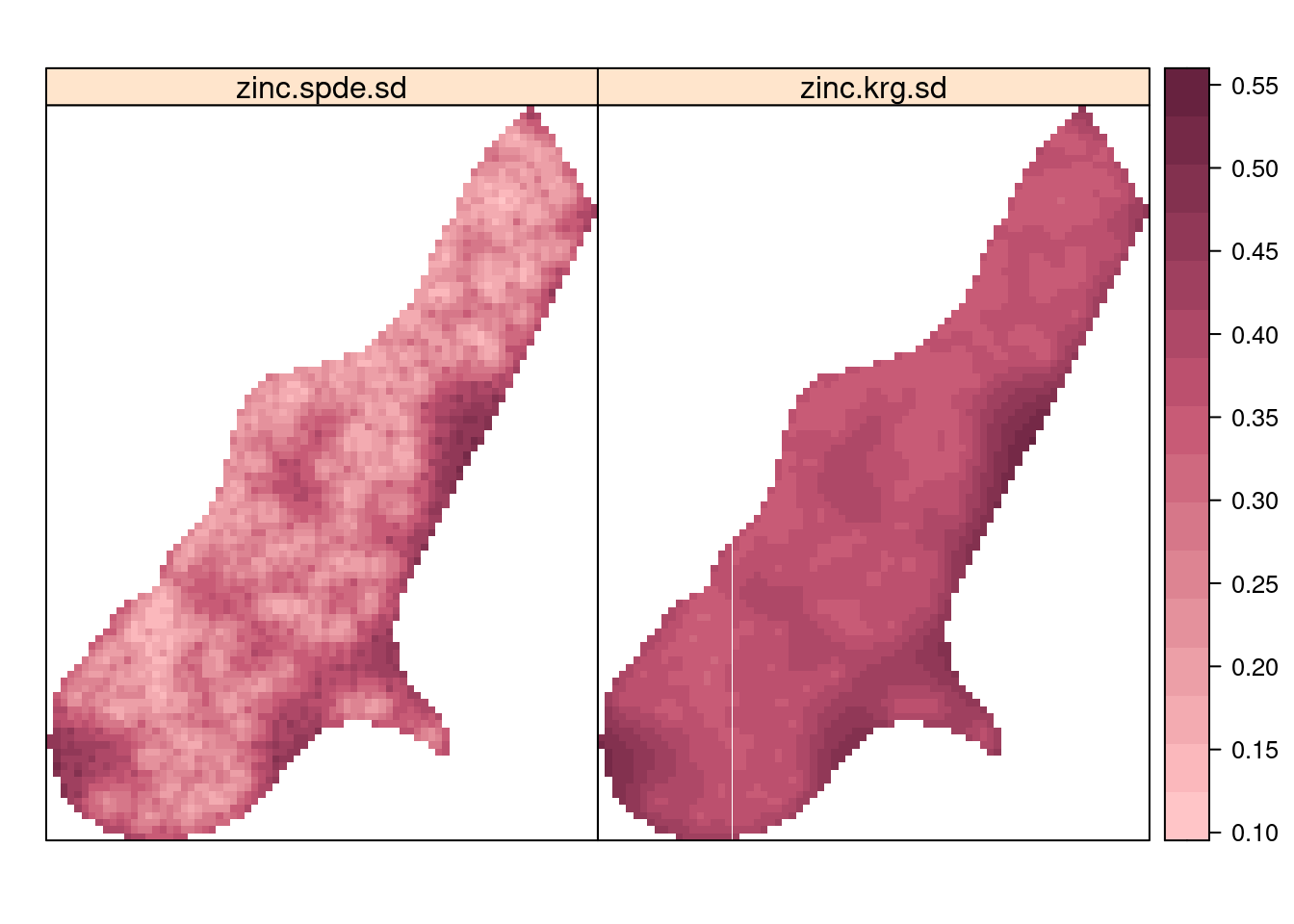
Figure 7.11: Posterior prediction standard deviations of log-concentration of zinc.

Besides the estimation of the concentration of zinc, studying the underlying spatial process may be of interest. For this reason, it is important to study the estimates of the parameters of the spatial effect. INLA reports summary estimates of the parameters in the internal scale, but the marginals of the variance and range parameters can be obtained using function inla.spde2.result. Then, summary statistics on the parameters using their respective posterior marginals can be computed with function inla.zmarginal. 

#Compute statistics in terms or range and variance
spde.est <- inla.spde2.result(inla = m1, name = "spatial.field",
  spde = meuse.spde, do.transf = TRUE)

#Kappa
#inla.zmarginal(spde.est$marginals.kappa[[1]])
#Variance
inla.zmarginal(spde.est$marginals.variance.nominal[[1]])
## Mean            0.243931 
## Stdev           0.0578992 
## Quantile  0.025 0.152402 
## Quantile  0.25  0.202374 
## Quantile  0.5   0.236094 
## Quantile  0.75  0.27715 
## Quantile  0.975 0.378597
#Range
inla.zmarginal(spde.est$marginals.range.nominal[[1]])
## Mean            416.358 
## Stdev           132.805 
## Quantile  0.025 221.148 
## Quantile  0.25  321.188 
## Quantile  0.5   393.715 
## Quantile  0.75  487.098 
## Quantile  0.975 737.859

A similar summary for the variogram used in the universal kriging can be obtained as follows:

#Summary stats; nugget is a 'random' effect with a variance
fit.vgm
##   model   psill range
## 1   Nug 0.07643   0.0
## 2   Sph 0.20529 728.7

The sill and range of the variogram are very similar to the estimates obtained for the Matérn covariance computed using SPDE. The nugget effect in the variogram can be regarded as a measurement error or the variance in the Gaussian likelihood. A rough comparison can be done between the sill of the nugget effect in the variogram and the inverse of the mode of the precision of the Gaussian likelihood:

#Precision of nugget term (similar to precision of error term)
1 / fit.vgm$psill[1]
## [1] 13.08

The resulting value is very similar to the posterior mean of the precision of the Gaussian likelihood. Hence, both universal kriging and the SPDE model provide similar estimates of the underlying spatial process.

As a final remark, it is worth mentioning that the inlabru package (Bachl et al. 2019) can simplify the way in which the model is defined and fit. Furthermore, the meshbuilder() function in the INLA package can help to define and assess the adequacy of a mesh in an interactive way (Krainski et al. 2018).

7.4 Point patterns

In Section 7.2 we considered the analysis of a point pattern using a discrete representation of the process. However, point patterns can also be studied as a continuous process. In particular, we will consider inhomogeneous Poisson point processes defined by a given intensity \(\lambda(x)\) which varies spatially and may also be modulated by some covariates.

Hence, the intensity can be represented as

\[ \lambda (x) = \lambda_0(x) \exp(\mathbf{\beta} \mathbf{x}) \]

Here, \(\lambda_0(x)\) is an underlying spatial distribution modulated by a vector of covariates \(\mathbf{x}\) with associated coefficients \(\mathbf{\beta}\).

The intensity can be estimated semi-parametrically by using a non-parametric estimate of \(\lambda_0(x)\) (Diggle 2013). For example, Diggle et al. (2007) use kernel smoothing to estimate \(\lambda_0(x)\) and a logistic regression (conditional of the locations of the observed events) to obtain estimates of the vector of coefficients \(\mathbf{\beta}\). Below we will show how to model \(\log(\lambda(x))\) using a Gaussian process to define a log-Gaussian Cox process (Krainski et al. 2018).

7.4.1 Log-Gaussian Cox processes

Simpson et al. (2016) describe the use of SPDE to estimate \(\lambda(x)\) using log-Gaussian Cox models. In particular, \(\lambda_0(x)\) is estimated using a SPDE, i.e.,

\[ \log(\lambda_0(x)) = S(x) \]

Here, \(S(x)\) is a stationary and isotropic Gaussian spatial process with a Matérn covariance. This spatial process can be estimated using the SPDE approach described in Section 7.3.

Simpson et al. (2016) show how fitting the previous model is similar to fitting a Poisson process on an extended data set using the locations of the events and the integration points of the SPDE mesh. This extended dataset needs to be created as follows:

  • The value of the response is 0 at the integration points and 1 at the observed points.

  • Each data point will have an associated weight, which will be 0 for the observed data and the area of its associated polygon in a Voronoi tessellation using the integration points.

  • Weights required to estimate the model (see below).

The inlabru package (Bachl et al. 2019) provides a simple interface for the analysis of point patterns with INLA and SPDE models. However, we provide here full details on the whole process to fit the model according to Simpson et al. (2016). The construction of the expanded dataset as well as the steps required for model fitting are described in the next example. The meshbuilder() function in the INLA package can also be used to test the adequacy of the mesh created for a SPDE latent effect (see also Krainski et al. 2018).

7.4.2 Castilla-La Mancha forest fires

The clmfires dataset in the spatstat package records the occurrence of forest fires in the region of Castilla-La Mancha (Spain) from 1998 to 2007. This dataset has been put together by Prof. Jorge Mateu. and Table 7.7 provides a summary of the variables in the dataset.

Table 7.7: Summary of variables in the clmfires dataset.
Variable Description
cause Cause of the fire (lightning, accident, intentional or other)
burnt.area Total area burned (in hectares)
date Date of fire
julian.date Date of fire, as days elapsed since 1 January 1998

Furthermore, the clmfires.extra dataset contains two objects with covariate information for the study region. These two objects are named clmcov100 and clmcov200 because they provide the information in several im objects (that represents raster data in the spatstat package) in a raster of size 100x100 and 200x200 pixels, respectively. Each one is a named list of four im objects with the variables in Table 7.8. Covariate landuse is a factor with levels: ‘urban’, ‘farm’ (which includes farms and orchards), ‘meadow’, ‘denseforest’, ‘conifer’ (which includes conifer forests and plantations), ‘mixedforest’, ‘grassland’, ‘bush’, ‘scrub’ and ‘artifgreen’ (such as golf courts).

Table 7.8: Summary of variables in the clmfires.extra dataset.
Variable Description
elevation Elevation of the terrain (in meters).
orientation Orientation of the terrain (in degrees).
slope Slope.
landuse Land use (a factor, see text for details).

First of all, the data will be loaded and the observed points in the period 2004 to 2007 selected. This is done because of the concern about how the location of the fires was done prior to 2004.

library("spatstat")
data(clmfires)

#Subset to 2004 to 2007
clmfires0407 <- clmfires[clmfires$marks$date >= "2004-01-01"]

Next, given that the pixels classified as artifgreen are just a few, we have merged this category with urban (because both are human-built):

# Set `urban` instead of `artifgreen`
idx <- which(clmfires.extra$clmcov100$landuse$v %in% c("artifgreen",
  "farm"))
clmfires.extra$clmcov100$landuse$v[idx] <- "urban"

# Convert to factor
clmfires.extra$clmcov100$landuse$v <- 
factor(as.character(clmfires.extra$clmcov100$landuse$v))
# Set right dimension of raster object

dim(clmfires.extra$clmcov100$landuse$v) <- c(100, 100)

Note that the reference category now is bush so the effects of all the other levels will be relative to this category (unless the intercept is removed from the model):

clmfires.extra$clmcov100$landuse
## factor-valued pixel image
## factor levels:
## [1] "bush"        "conifer"     "denseforest" "grassland"   "meadow"     
## [6] "mixedforest" "scrub"       "urban"      
## 100 x 100 pixel array (ny, nx)
## enclosing rectangle: [-2.1, 397.9] x [-2.1, 397.9] kilometres

Covariates elevation and orientation are rescaled so that they are expressed in kilometers and radians. This is done in order to avoid problems when fitting the spatial model with INLA. This is particularly important for elevation because it is originally in meters.

#In addition, we will rescale `elevation` (to express it in kilometers) and
#`orientation` (to be in radians) so that fixed effects are better estimated:
clmfires.extra$clmcov100$elevation <- 
  clmfires.extra$clmcov100$elevation / 1000
clmfires.extra$clmcov100$orientation <- 
  clmfires.extra$clmcov100$orientation * pi / 180

Juan, Mateu, and Díaz-Avalos (2010) provide an analysis of the forest fires in 1998 alone and they suggest analyzing this type of data using log-Gaussian Cox processes. In addition, they show that forest fires due to lightning have a different pattern. Hence, we will focus our analysis of these type of fires and subset these points from the original dataset:

clmfires0407 <- clmfires0407[clmfires0407$marks$cause == "lightning", ]

Figure 7.12 shows the boundary of Castilla-La Mancha and the location of the forest fires due to lightning. Note how most of them appear in the east part of the region.

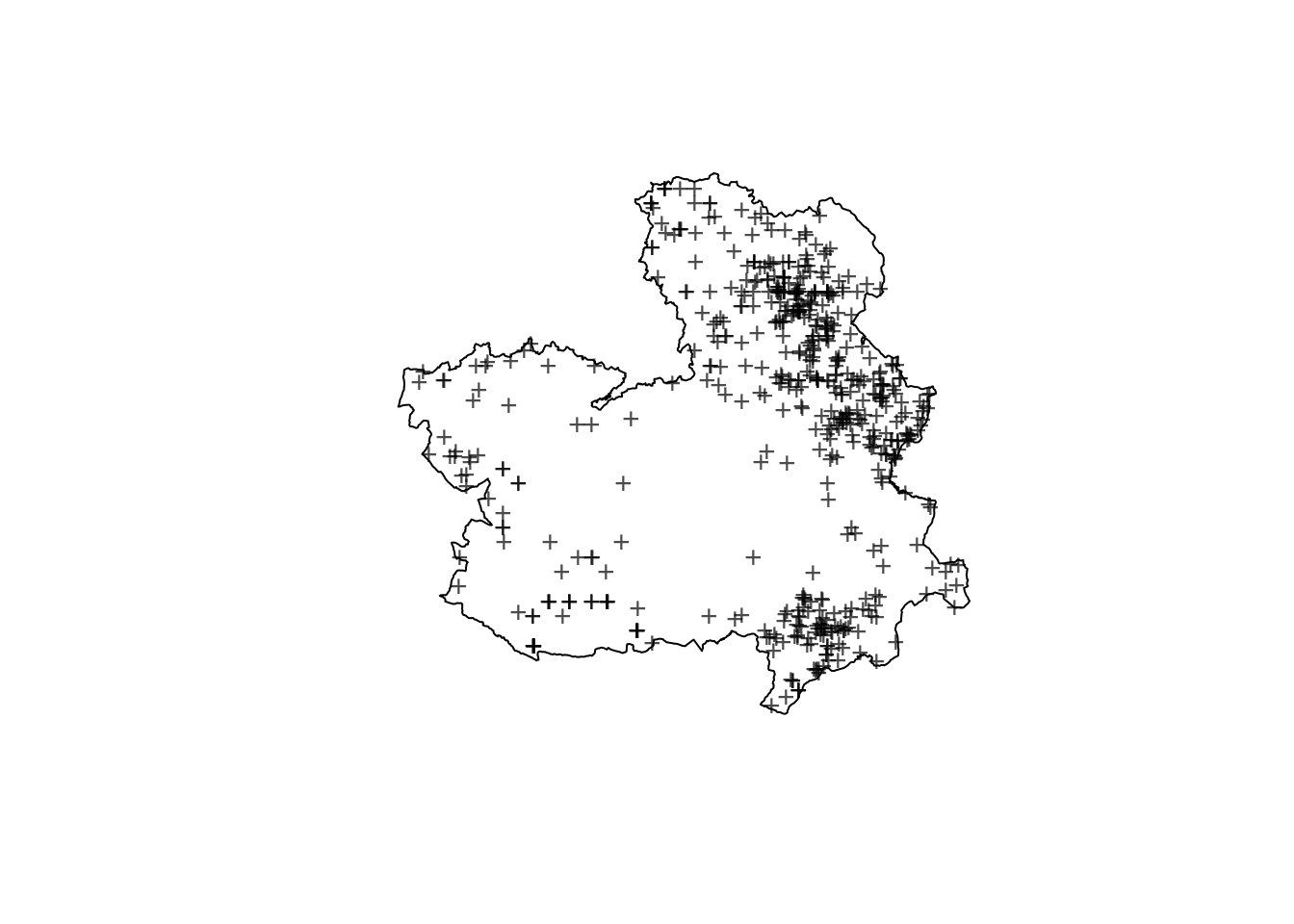
Location of forest fires due to a lightning in Castilla-La Mancha in the period.

Figure 7.12: Location of forest fires due to a lightning in Castilla-La Mancha in the period.

Next, the boundary of the study region will be extracted from the ppp object and it will be used to create a mesh over the study region. This mesh will be used to estimate the latent stationary and isotropic Gaussian process with Matérn covariance using the SPDE approach in INLA.

clm.bdy <- do.call(cbind, clmfires0407$window$bdry[[1]])
#Define mesh
clm.mesh <- inla.mesh.2d(loc.domain = clm.bdy, max.edge = c(15, 50),
  offset = c(10, 10))

As discussed before, model fitting requires an expanded dataset with the locations of the forest fires and the integration points in the mesh.

#Points
clm.pts <- as.matrix(coords(clmfires0407))
clm.mesh.pts <- as.matrix(clm.mesh$loc[, 1:2])
allpts <- rbind(clm.mesh.pts, clm.pts)

# Number of vertices in the mesh
nv <- clm.mesh$n
# Number of points in the data
n <- nrow(clm.pts)

Next, the SPDE latent effect needs to be defined. In this case, penalized complexity priors (see Section 5.4) are used for the range and standard deviation of the Matérn covariance. In particular, the prior of the range \(r\) is set by defining \((r_0, p_r)\) such that

\[ P(r < r_0) = p_r. \]

Similarly, the penalized complexity prior for the standard deviation \(\sigma\) is defined by pair \((\sigma_0, p_s)\), such that

\[ P(\sigma >\sigma_0) = p_s. \]

As a prior assumption the probability of the range being higher than 50 is small (i.e., \(r_0 = 50\) and \(p_r=0.9\)) and that the probability of \(\sigma\) being higher than 5 is also small (i.e., \(\sigma_0=1\) and \(p_s = 0.01\)). A SPDE latent effect with this type of prior is created with function inla.spde2.pcmatern() as follows: 

#Create SPDE
clm.spde <- inla.spde2.pcmatern(mesh = clm.mesh, alpha = 2,
  prior.range = c(50, 0.9), # P(range < 50) = 0.9
  prior.sigma = c(1, 0.01) # P(sigma > 10) = 0.01
)

See also Sørbye et al. (2019) for some comments on setting priors when fitting log-Gaussian Cox processes to point patterns using SPDEs.

The weights associated with the mesh points are equal to the area of the surrounding polygon in a Voronoi tessellation that falls inside the study region. This is computed below using packages deldir (Turner 2019), rgeos (R. Bivand and Rundel 2019) and SDraw (McDonald and McDonald 2019). Note that spatial data must be in one of the objects in the sp package and, for this reason, the boundary is converted into a SpatialPolygons object and function voronoi.polygons() is used as it returns the Voronoi tessellation as a SpatialPolygons object as well.

library("deldir")
library("SDraw")
 
# Voronoi polygons (as SpatialPolygons)
mytiles <- voronoi.polygons(SpatialPoints(clm.mesh$loc[, 1:2]))

# C-LM bounday as SpatialPolygons
clmbdy.sp <- SpatialPolygons(list(Polygons(list(Polygon (clm.bdy)),
  ID = "1"))) 

#Compute weights
require(rgeos)

w <- sapply(1:length(mytiles), function(p) {
  aux <- mytiles[p, ]  

  if(gIntersects(aux, clmbdy.sp) ) {
    return(gArea(gIntersection(aux, clmbdy.sp)))
  } else {
    return(0)
  }
})

Note how the sum of the weights is equal to the area of the study region:

# Sum of weights
sum(w)
## [1] 79355
# Area of study region
gArea(clmbdy.sp)
## [1] 79355

Figure 7.13 shows the mesh points (black dots) as well as the resulting Voronoi tessellation and the boundary of Castilla-La Mancha. The weight associated with each point is the area of the associated Voronoi polygon inside the region of Castilla-La Mancha.

Voronoi tesselletation used in the analysis of forest fires in Castilla-La Mancha.

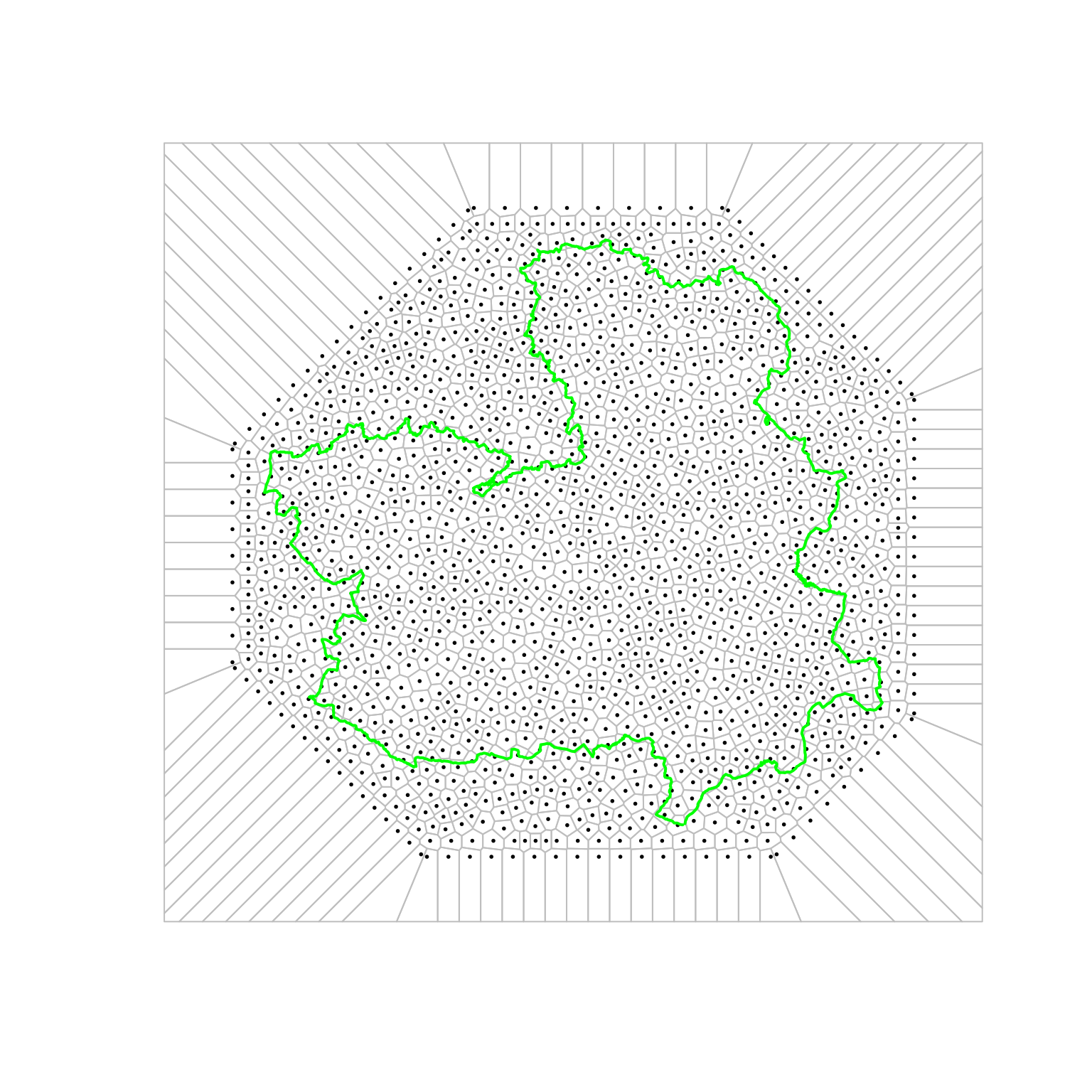
Figure 7.13: Voronoi tesselletation used in the analysis of forest fires in Castilla-La Mancha.

Once the weights associated with the mesh points have been computed, the expanded dataset can be put together. Values of the covariates at the integration points are required to fit the model. These are obtained from the raster data available in the clmfires.extra dataset.

#Prepare data
y.pp = rep(0:1, c(nv, n))
e.pp = c(w, rep(0, n))

lmat <- inla.spde.make.A(clm.mesh, clm.pts)
imat <- Diagonal(nv, rep(1, nv))

A.pp <-rbind(imat, lmat)

clm.spde.index <- inla.spde.make.index(name = "spatial.field",
  n.spde = clm.spde$n.spde)

Covariates required in the analysis are obtained by using different functions in the spatstat package. In particular, function nearest.pixel() is used below to assign to each point (in the expanded dataset) the values of the covariates of the nearest pixel in the raster object.

#Covariates
allpts.ppp <- ppp(allpts[, 1], allpts[, 2], owin(xrange = c(-15.87, 411.38), 
  yrange = c(-1.44, 405.19)))

# Assign values of covariates to points using value of nearest pixel
covs100 <- lapply(clmfires.extra$clmcov100, function(X){
  pixels <- nearest.pixel(allpts.ppp$x, allpts.ppp$y, X)
  sapply(1:npoints(allpts.ppp), function(i) {
    X[pixels$row[i], pixels$col[i]]
  })
})

# Intercept for spatial model
covs100$b0 <- rep(1, nv + n)

Once all the required data have been obtained, the data stack for model fitting is created:

#Create data structure
clm.stack <- inla.stack(data = list(y = y.pp, e = e.pp),
  A = list(A.pp, 1), 
  effects = list(clm.spde.index, covs100),
  tag = "pp")

Similarly, another stack of data will be put together for prediction. This will require the locations of the points in a regular grid as well as the values of the covariates at the grid points (now using the subsetting operator in the spatstat package). The grid used will be the same as the one used in the raster data with the covariates.

#Data structure for prediction
library("maptools")
sgdf <- as(clmfires.extra$clmcov100$elevation, "SpatialGridDataFrame")
sp.bdy <- as(clmfires$window, "SpatialPolygons")
idx <- over(sgdf, sp.bdy)
spdf <- as(sgdf[!is.na(idx), ], "SpatialPixelsDataFrame")

pts.pred <- coordinates(spdf)
n.pred <- nrow(pts.pred)

#Get covariates (using subsetting operator in spatstat)
ppp.pred <- ppp(pts.pred[, 1], pts.pred[, 2], window = clmfires0407$window)
covs100.pred <- lapply(clmfires.extra$clmcov100, function(X) {
  X[ppp.pred]
})

# Intercept for spatial model
covs100.pred$b0 <- rep(1, n.pred)

#Prediction points
A.pred <- inla.spde.make.A (mesh = clm.mesh, loc = pts.pred)
clm.stack.pred <- inla.stack(data = list(y = NA),
   A = list(A.pred, 1),
   effects = list(clm.spde.index, covs100.pred), 
   tag = "pred")

Finally, all data stacks will be put together into a single object:

#Join data
join.stack <- inla.stack(clm.stack, clm.stack.pred)

Model fitting will be carried out similarly as in the geostatistics case. However, now the likelihood to be used in a Poisson and the weights associated to the points in the expanded dataset need to be passed using parameter E. The integration strategy is set to "eb" in order to reduce computation time (Krainski et al. 2018).

The first model estimates the intensity of the point process using an intercept and the SPDE latent effect. This estimate should be similar to a kernel density smoothing (Gómez-Rubio, Cameletti, and Finazzi 2015).

pp.res0 <- inla(y ~ 1 + 
    f(spatial.field, model = clm.spde), 
  family = "poisson", data = inla.stack.data(join.stack),
  control.predictor = list(A = inla.stack.A(join.stack), compute = TRUE,
    link = 1),
  control.inla = list(int.strategy = "eb"),
  E = inla.stack.data(join.stack)$e)

Next, the model is defined to include covariates and the SPDE latent effect.

pp.res <- inla(y ~ 1 + landuse + elevation + orientation + slope +
    f(spatial.field, model = clm.spde), 
  family = "poisson", data = inla.stack.data(join.stack),
  control.predictor = list(A = inla.stack.A(join.stack), compute = TRUE,
    link = 1), verbose = TRUE,
  control.inla = list(int.strategy = "eb"),
  E = inla.stack.data(join.stack)$e)
summary(pp.res)
## 
## Call:
##    c("inla(formula = y ~ 1 + landuse + elevation + orientation + 
##    slope + ", " f(spatial.field, model = clm.spde), family = 
##    \"poisson\", data = inla.stack.data(join.stack), ", " E = 
##    inla.stack.data(join.stack)$e, verbose = TRUE, control.predictor = 
##    list(A = inla.stack.A(join.stack), ", " compute = TRUE, link = 1), 
##    control.inla = list(int.strategy = \"eb\"))" ) 
## Time used:
##     Pre = 0.801, Running = 75.3, Post = 1.2, Total = 77.3 
## Fixed effects:
##                      mean    sd 0.025quant 0.5quant 0.975quant   mode kld
## (Intercept)        -2.845 0.304     -3.441   -2.845     -2.249 -2.845   0
## landuseconifer      0.051 0.209     -0.360    0.051      0.462  0.051   0
## landusedenseforest  0.517 0.256      0.007    0.519      1.014  0.523   0
## landusegrassland    0.222 0.237     -0.247    0.223      0.683  0.226   0
## landusemeadow       0.279 0.344     -0.416    0.286      0.936  0.300   0
## landusemixedforest  0.750 0.246      0.265    0.751      1.231  0.752   0
## landusescrub        0.386 0.199     -0.004    0.385      0.777  0.385   0
## landuseurban        0.211 0.182     -0.142    0.209      0.573  0.206   0
## elevation           0.117 0.348     -0.569    0.119      0.795  0.121   0
## orientation        -0.020 0.029     -0.077   -0.020      0.037 -0.020   0
## slope              -0.017 0.009     -0.036   -0.017      0.001 -0.017   0
## 
## Random effects:
##   Name     Model
##     spatial.field SPDE2 model
## 
## Model hyperparameters:
##                           mean     sd 0.025quant 0.5quant 0.975quant
## Range for spatial.field 120.58 22.767     84.255   117.61     173.22
## Stdev for spatial.field   1.27  0.185      0.957     1.25       1.68
##                           mode
## Range for spatial.field 111.32
## Stdev for spatial.field   1.21
## 
## Expected number of effective parameters(stdev): 101.90(0.00)
## Number of equivalent replicates : 21.35 
## 
## Marginal log-Likelihood:  -3072.82 
## Posterior marginals for the linear predictor and
##  the fitted values are computed

The summary of the model with covariates provides some insight on the factors associated to the location of forest fires in this region. Elevation, orientation and slope do not seem to have an effect. Regarding land use, bush is the baseline and it does not seem that there are differences with most of the different types of land use. However, dense and mixed forest (and, perhaps, scrub) seem to have an increased number of forest fires due to lightning as compared to the baseline level.

The fitted values of the intensity with both models can be retrieved from the model fits and added to the SpatialPixelsDataFrame with the data to be plotted:

#Prediction
idx <- inla.stack.index(join.stack, 'pred')$data
# MOdel with no covariates
spdf$SPDE0 <- pp.res0$summary.fitted.values[idx, "mean"]
#Model with covariates
spdf$SPDE <- pp.res$summary.fitted.values[idx, "mean"]

Figure 7.14 displays the posterior means of the estimated intensity at the grid points for both models and it can be used to assess fire risk. For example, a region of high risk can be found in the southeast part of Castilla-La Mancha (municipalities of Yeste, Letur and Nerpio).

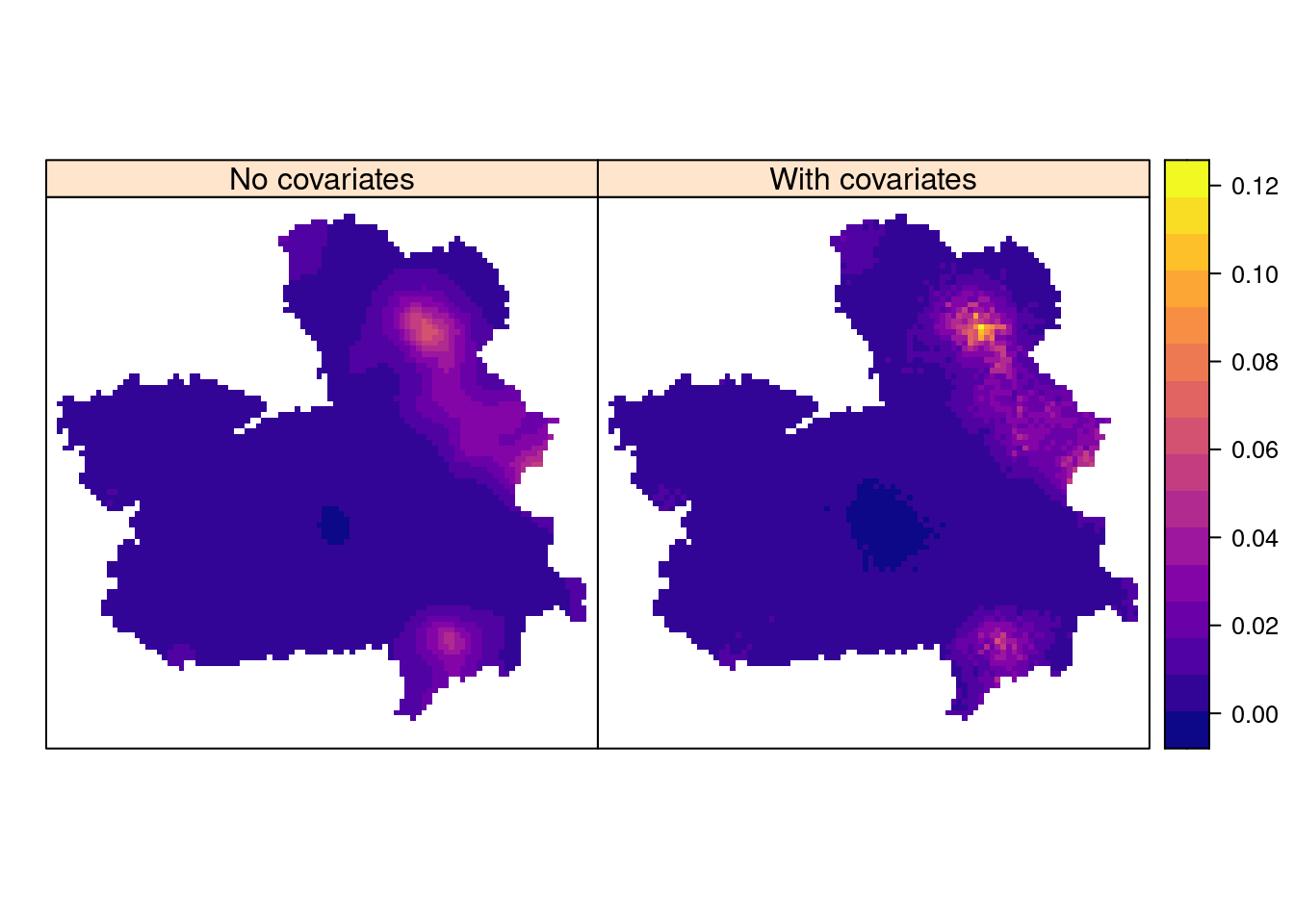
Intensity of forest fires in Castilla-La Mancha (Spain). The region is about 400 x 400 km.

Figure 7.14: Intensity of forest fires in Castilla-La Mancha (Spain). The region is about 400 x 400 km.

In order to understand the latent spatial pattern, the marginals of its parameters can be estimated similarly as in the geostatistics example:

#Compute statistics in terms or range and variance
spde.clm.est <- inla.spde2.result(inla = pp.res, name = "spatial.field",
  spde = clm.spde, do.transf = TRUE)

#Variance
inla.zmarginal(spde.clm.est$marginals.variance.nominal[[1]])
## Mean            1.6395 
## Stdev           0.486537 
## Quantile  0.025 0.918128 
## Quantile  0.25  1.29075 
## Quantile  0.5   1.5578 
## Quantile  0.75  1.90123 
## Quantile  0.975 2.81266
#Range
inla.zmarginal(spde.clm.est$marginals.range.nominal[[1]])
## Mean            120.544 
## Stdev           22.5798 
## Quantile  0.025 84.384 
## Quantile  0.25  104.34 
## Quantile  0.5   117.562 
## Quantile  0.75  133.71 
## Quantile  0.975 172.63

Note that the output from the model already provided summary statistics for the range and variance of the spatial process. According to the value of the spatial range, it seems that the spatial random effect accounts for medium-scale spatial variation (remember that the region covers an area of about 400 x 400 km). The estimate of the spatial variance seems to be small, which makes the spatial variation not have too extreme peaks.

References

Bachl, Fabian E., Finn Lindgren, David L. Borchers, and Janine B. Illian. 2019. “inlabru: An R Package for Bayesian Spatial Modelling from Ecological Survey Data.” Methods in Ecology and Evolution 10: 760–66. https://doi.org/10.1111/2041-210X.13168.

Baddeley, Adrian, Ege Rubak, and Rolf Turner. 2015. Spatial Point Patterns: Methodology and Applications with R. London: Chapman; Hall/CRC Press. http://www.crcpress.com/Spatial-Point-Patterns-Methodology-and-Applications-with-R/Baddeley-Rubak-Turner/9781482210200/.

Banerjee, S., B. P. Carlin, and A. E. Gelfand. 2014. Hierarchical Modeling and Analysis for Spatial Data. 2nd ed. Boca Raton, FL: Chapman & Hall/CRC.

Bivand, Roger, and Colin Rundel. 2019. Rgeos: Interface to Geometry Engine - Open Source (’Geos’). https://CRAN.R-project.org/package=rgeos.

Bivand, Roger S. 2017. “Revisiting the Boston Data Set - Changing the Units of Observation Affects Estimated Willingness to Pay for Clean Air.” REGION 1 (4): 109–27. http://openjournals.wu.ac.at/ojs/index.php/region/article/view/107.

Bivand, Roger S., Virgilio Gómez-Rubio, and Håvard Rue. 2015. “Spatial Data Analysis with R-INLA with Some Extensions.” Journal of Statistical Software 63 (20): 1–31. http://www.jstatsoft.org/v63/i20/.

Bivand, Roger S., Edzer Pebesma, and Virgilio Gómez-Rubio. 2013. Applied Spatial Data Analysis with R. 2nd ed. New York: Springer.

Bivand, Roger, and David W. S. Wong. 2018. “Comparing Implementations of Global and Local Indicators of Spatial Association.” TEST 27 (3): 716–48. https://doi.org/10.1007/s11749-018-0599-x.

Blangiardo, Marta, and Michela Cameletti. 2015. Spatial and Spatio-Temporal Bayesian Models with R-INLA. Chichester, UK: John Wiley & Sons Ltd.

Condit, R. 1998. Tropical Forest Census Plots. Springer-Verlag Berlin Heidelberg.

Condit, R., S. P. Hubbell, and R. B. Foster. 1996. “Changes in Tree Species Abundance in a Neotropical Forest: Impact of Climate Change.” Journal of Tropical Ecology 12: 231–56.

Cressie, Noel. 2015. Statistics for Spatial Data. Revised. Hoboken, New Jersey: John Wiley & Sons, Inc.

Cressie, Noel, and Christopher K. Wikle. 2011. Statistics for Spatio-Temporal Data. Hoboken, New Jersey: John Wiley & Sons, Inc.

Diggle, Peter J. 2013. Statistical Analysis of Spatial and Spatio-Temporal Point Patterns. 3rd ed. Chapman; Hall/CRC Press.

Diggle, Peter J., Virgilio Gómez‐Rubio, Patrick E. Brown, Amanda G. Chetwynd, and Susan Gooding. 2007. “Second‐Order Analysis of Inhomogeneous Spatial Point Processes Using Case–Control Data.” Biometrics 2 (63): 550–57.

Gilley, O. W., and R. Kelley Pace. 1996. “On the Harrison and Rubinfeld Data.” Journal of Environmental Economics and Management 31: 403–5.

Gómez-Rubio, Virgilio, Michela Cameletti, and Francesco Finazzi. 2015. “Analysis of Massive Marked Point Patterns with Stochastic Partial Differential Equations.” Spatial Statistics 14: 179–96. https://doi.org/https://doi.org/10.1016/j.spasta.2015.06.003.

Harrison, David, and Daniel L. Rubinfeld. 1978. “Hedonic Housing Prices and the Demand for Clean Air.” Journal of Environmental Economics and Management 5: 81–102.

Hubbell, S. P., and R. B. Foster. 1983. “Diversity of Canopy Trees in a Neotropical Forest and Implications for Conservation.” In Tropical Rain Forest: Ecology and Management, edited by S. L. Sutton, T. C. Whitmore, and A. C. Chadwick, 25–41. Oxford: Blackwell Scientific Publications.

Juan, P., J. Mateu, and C. Díaz-Avalos. 2010. “Characterizing Spatial-Temporal Forest Fire Patterns.” In METMA V: International Workshop on Spatio-Temporal Modelling. Santiago de Compostela, Spain.

Krainski, Elias T., Virgilio Gómez-Rubio, Haakon Bakka, Amanda Lenzi, Daniela Castro-Camilo, Daniel Simpson, Finn Lindgren, and Håvard Rue. 2018. Advanced Spatial Modeling with Stochastic Partial Differential Equations Using R and INLA. Boca Raton, FL: Chapman & Hall/CRC.

Leroux, B., X. Lei, and N. Breslow. 1999. “Estimation of Disease Rates in Small Areas: A New Mixed Model for Spatial Dependence.” In Statistical Models in Epidemiology, the Environment and Clinical Trials, edited by M Halloran and D Berry, 135–78. New York: Springer-Verlag.

Lindgren, Finn, Håvard Rue, and Joham Lindström. 2011. “An Explicit Link Between Gaussian Fields and Gaussian Markov Random Fields: The Stochastic Partial Differential Equation Approach (with Discussion).” Journal of the Royal Statistical Society, Series B 73 (4): 423–98.

Lovelace, Robin, Jakub Nowosad, and Jannes Muenchow. 2019. Geocomputation with R. Boca Raton, FL: Chapman & Hall/CRC.

McDonald, Trent, and Aidan McDonald. 2019. SDraw: Spatially Balanced Samples of Spatial Objects. https://CRAN.R-project.org/package=SDraw.

Møller, J., and R. P. Waagepetersen. 2007. “Modern Spatial Point Process Modelling and Inference (with Discussion).” Scandinavian Journal of Statistics 34: 643–711.

Pebesma, E. J. 2004. “Multivariable Geostatistics in S: The Gstat Package.” Computers & Geosciences 30: 683–91.

Simpson, Daniel, Janine B. Illian, S. H. Sørbye, and Håvard Rue. 2016. “Going Off Grid: Computationally Efficient Inference for Log-Gaussian Cox Processes.” Biometrika 1 (103): 49–70.

Sørbye, Sigrunn H., Janine B. Illian, Daniel P. Simpson, David Burslem, and Håvard Rue. 2019. “Careful Prior Specification Avoids Incautious Inference for Log-Gaussian Cox Point Processes.” Journal of the Royal Statistical Society: Series C (Applied Statistics) 68 (3): 543–64. https://doi.org/10.1111/rssc.12321.

Turner, Rolf. 2019. Deldir: Delaunay Triangulation and Dirichlet (Voronoi) Tessellation. https://CRAN.R-project.org/package=deldir.

Ugarte, M. D., A. Adin, T. Goicoa, and A. F. Militino. 2014. “On Fitting Spatio-Temporal Disease Mapping Models Using Approximate Bayesian Inference.” Statistical Methods in Medical Research 23: 507–30. https://doi.org/10.1177/0962280214527528.